Professeur honoraire à la Sorbonne
(1876-1952)

“La notion de problème
en philosophie.”

Un article publié dans un ouvrage de l’auteur intitulé Études de philosophie antique, 1955, pp. 10-16. Paris : Les Presses universitaires de France.

Note :

On indique entre crochets [XX] le nombre correspondant à l’édition papier originelle.

[10]

Le mot problème est employé de nos jours avec une singulière fréquence. La moindre difficulté se présente-t-elle, on en fait un problème : problème colonial, problème fiscal, problème du ravitaillement et tant d’autres, nous sommes assiégés quotidiennement par ces expressions ; on croirait que, en empruntant le mot aux sciences exactes, on pense mettre plus de rigueur dans la position des difficultés et être ainsi un peu plus près de les résoudre. Les philosophes ne sont pas les derniers à l’employer ; dans tous les cas où l’on usait naguère des mots théorie ou doctrine, on trouve aujourd’hui le mot plus modeste de problème : problème de l’être, problème de la connaissance, de la science, problème moral, problème religieux. Les philosophes allemands emploient souvent le mot Problematik pour désigner une discipline concernant la manière de poser les problèmes. Il est tout naturel que le succès de cette expression ait amené la réunion de l’Institut international de Philosophie en 1947, à Lund, à prendre comme thème : Le problème du problème ; il est possible en effet que ce succès même dénote un caractère assez important de l’orientation philosophique actuelle.

Dans l’Antiquité le mot n'était guère employé que par les mathématiciens dans le sens technique qu'il a gardé. Si nous ouvrons le Commentaire sur Euclide de Proclus [1], qui est fort bien informé de l'histoire des mathématiques, nous y trouvons que, par opposition au théorème qui se propose de déduire une propriété d'un être mathématique de son essence, donnée dans [11] la définition, le problème cherche à construire une grandeur dans ses relations avec d’autres (par exemple diviser une droite en moyenne et extrême raison), et la solution nous fait assister à la genèse de cette grandeur. L’expression s'étend à l'astronomie mathématique, et Platon lui-même l'emploie dans la République [2] pour désigner la recherche de la combinaison des cercles à mouvement uniforme qui doivent expliquer I'apparence du mouvement varié des planètes ; mais un Platonicien comme Speusippe répugne à I'employer et veut que tout en géométrie soit théorème ; car le problème nous annonce la génération d'une grandeur, et « il n'y a pas de génération dans les choses éternelles » [3]. Il y a, dans la collection d'Aristote, une compilation, intitulée Problèmes, dont la date est tardive (V^e ou VI^e siècle, estime Léon Robin), et dont le titre par conséquent n'est pas d'Aristote ; il contient, à côté de problèmes mathématiques, des questions relatives à la biologie et à la morale. Mais toujours, comme en mathématiques, le problème se rapporte à une question concrète, limitée, définie, dont la position même suppose la préexistence de la science à l'intérieur de laquelle il est posé, science qui donnera les moyens de le résoudre. Le problème n'a qu'une place restreinte.

Il y a pourtant une exception, et elle est de grande importance : dans les Topiques, cette oeuvre consacrée à l’art de la discussion, Aristote définit ainsi le problème [4] : « La différence du problème et de la proposition tient à la manière dont est posée la question. Si on dit par exemple : animal pédestre et bipède est la définition de l'homme, n'est-ce pas ? on obtient une proposition. Si, par contre, on dit : est-ce que animal pédestre et bipède est, ou non, la définition de l'homme ? c'est là un problème ». Autrement dit, tandis que la définition n'envisage qu'une thèse que l'on demande d'admettre, le problème considère comme possible le contraire de la thèse proposée, et il appelle à la fois l'examen des arguments en faveur de cette thèse et contre elle ; il est essentiellement dialectique, et par là bien utile à la philosophie puisque « la possibilité d'apporter aux problèmes des arguments dans les deux sens nous fera [12] découvrir plus facilement la vérité et l’erreur dans chaque cas ». Le problème est donc avant tout conscience d’une alternative [5] ; il oppose l’esprit à lui-même. Et nous avons sans doute ici un de points de départ de la philosophie. La philosophie a commencé lorsque les affirmations de la conscience spontanée sur l’univers sont devenues problématiques.

Le charpentier, l’architecte, le sculpteur savent ce qu’est la matière sur laquelle ils travaillent : le laboureur, le marin savent ce que sont les éléments, la terre, la mer, l’atmosphère, qui leur résistent ou leur sont favorables ; l’homme religieux qui est, par les rites, en rapport avec son dieu, est assuré de son existence ; et toutes ces relations vitales (au sens plein du mot) engendrent bien chez eux une foule variée de problèmes pratiques que peut seule résoudre l’expérience ; mais nul d’entre eux ne songe à poser, à l’égard de ces objets qui occupent leur vie entière, les problèmes philosophiques que se sont posés les Ioniens ou leurs successeurs : Qu’est-ce que la matière ? Quelle est l’origine des éléments ? Les dieux existent-ils et quelle est leur nature ? C’est que, aux yeux de nul d’entre eux, il n’y a d’alternative : la matière, les éléments, le dieu s’imposent comme des réalités indiscutables. Pour qu’il y ait problème, il faut commencer par douter que ces réalités soient bien foncièrement ce qu’elles paraissent être, qu’elles aient toujours la forme qu’elles ont maintenant, par se demander si Dieu existe et quelle est sa nature ; il faut, en un mot, qu’il y ait une alternative : la matière est-elle cela ou non ? Dieu existe-t-il ou non ?

On voit que, comme le problème mathématique suppose une science antérieure à lui, le problème dialectique suppose aussi un ensemble d’assertions au milieu desquelles il naît. Autrement dit le problématique suppose toujours du « métaproblématique ». Mais le métaproblématique n’est pas le même dans les deux cas ; dans la dialectique il n’est pas fait d’assertions scientifiques certaines, mais d’opinions plus on moins [13] probables selon qu'elles sont ou non traditionnelles, qu'elles sont celles de tous ou de quelques-uns, celles des sages ou des ignorants. Si l'on n'a pour résoudre le problème dialectique (c'est-à-dire pour choisir un des termes de l'alternative) que des matériaux de ce genre, il ne sera jamais résolu à la rigueur, et I'incertitude des prémisses se retrouvera dans la conclusion. La philosophie risquera alors d'en rester à l'exposition antithétique des raisons pro et contra, sans aucune conclusion ; c’est bien ce qui est arrivé chez les sophistes du V^e et du IV^e siècles, et le scepticisme postérieur, qui s'est renouvelé tant de fois jusqu'à nos jours, met sa complaisance dans cette situation ; même en dehors du scepticisme, l'exposé dialectique du pour et contre est au moins considéré comme un préliminaire indispensable de la philosophie, comme on le voit dans les articles successifs de la Somme théologique de saint Thomas, sans parler du pari de Pascal, de l'antithétique de la raison pure de Kant, des dilemmes de la Métaphysique de Renouvier. Le fameux exercice de la seconde partie du Parménide est, selon une interprétation à laquelle je m'associe pleinement, une stylisation de ce procédé dialectique, montrant que l'on peut tout affirmer et tout nier de la thèse de Parménide sur l'unité de l'être et du contraire de cette thèse.

La philosophie ne serait peut-être pas sortie de cette situation sans Socrate. Les dialogues socratiques de Platon nous montrent un Socrate, dialecticien certes, mais qui intériorise en quelque sorte le débat dialectique par l'examen qu'il fait de son interlocuteur ; il crée chez celui-ci la conscience pénible d'une contradiction intime ; le pour et le contre, au lieu d'être chacun soutenu par un adversaire distinct, se révèlent à la conscience comme intérieurs à elle-même, comme une dissociation qu'elle ne peut supporter. Le problème est alors de sortir de l'opinion instable, de réviser cette métaproblématique qui est responsable de cette incertitude. Le rôle de Socrate fut de faire sentir la contradiction intime comme une douleur et presque comme un remords. Le problème de la métaproblématique, ou, pour être plus clair, la découverte d'assertions philosophiques certaines, soustraites par leur nature à l'examen dialectique, ce fut là et cela reste sans doute le problème philosophique essentiel ; en faire l’histoire ce serait faire l’histoire de notre philosophie [14] tout entière : la vision platonicienne du Bien, les idées claires de Descartes, le fait primitif chez Maine de Biran, la structure dialectique de l'esprit chez Hegel, la valeur de la science dans le positivisme, l'intuition bergsonienne, tous ces facteurs originels de la pensée philosophique appartiennent à la métaproblématique. Les philosophies auxquelles nous nous référons sont des philosophies qui n'admettent pas l'alternative et dont le développement est fait, pourrait-on dire, de théorèmes plutôt que de problèmes [6]. Dans un aussi vaste sujet, je me contenterai de quelques remarques succinctes, pour éclairer les vues qui précèdent :

1. On sait quelles précautions il faut, en philosophie, pour poser un problème, et combien il est plus facile qu’ailleurs de glisser dans les pseudoproblèmes ou dans les problèmes insolubles. L’activité des plus grands penseurs, de Kant par exemple, s’est surtout employée à changer la position des problèmes, et il l’a changé quand il s’est aperçu que la métaproblématique, dont on attendait leur solution, les faisait évanouir plus qu’elle ne les résolvait. Par exemple, faire dépendre la solution du problème  moral de vues théorétiques sur la nature ou sur Dieu, c’est le faire évanouir, en négligeant le caractère essentiel de la volonté morale, l’autonomie [7]. Ici le problème disparaît par une sorte de 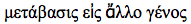 ; ailleurs, par exemple chez Condillac, il s’évanouit par une réduction abusive, lorsque les phénomènes les plus complexes de la conscience sont pris pour une sensation transformée. Comme on le voit par ces exemples, le danger, en philosophie, c’est de fausser le caractère original des problèmes, en les rapportant à une métaproblématique qui ne leur convient pas.

2. Cette remarque permet de comprendre toute la portée de l'assertion bien connue de Bergson : « En philosophie, un problème bien posé est un problème résolu ». Tandis que, en mathématiques, après avoir posé le problème, on cherche les données acquises dont la combinaison permettra de les résoudre, il semble bien en effet que, en philosophie, leur position même [15] n’est pas possible si on ne les voit dans le cadre de la métaproblématique qui leur convient. On ne trouve pas en philosophie cet ordre linéaire et progressif que l'on voit [8] en mathématiques ; la pensée philosophique est circulaire ; les problèmes qu'elle se pose et les principes par lesquels elle entend les résoudre sont mutuellement dépendants, sans qu'il y ait pour cela cercle vicieux. Que l'on songe, par exemple, aux problèmes de la genèse de l'intelligence et de la genèse de la matière dans l'Évolution créatrice ; ces problèmes ne seraient pas même posés, si nous n'avions l'intuition d’une certaine diminution ou chute de l'élan vital, intuition qui sert en même temps à les résoudre, mais qui, à son tour, est affermie et renforcée par cette solution même. Et pour prendre un exemple dans une philosophie d'une inspiration tout autre : le problème de la matière, qui est un vieux problème, ne serait pas résolu comme il l'est par Descartes, si celui-ci, dans sa métaproblématique, ne posait l'exigence, pour elle, d'être l'objet d'une idée claire et distincte ; mais le mécanisme universel, fondé sur cette solution, raffermit à son tour ce principe qui n'aurait aucun sens s'il restait sans application.

3. Ce que je viens de dire permettra de juger une thèse curieuse de M. Gabriel Marcel sur la « distinction du mystérieux et du problématique. Le problème est quelque chose qu’on rencontre, qui barre la route. II est tout entier devant moi. Au contraire, le mystère est quelque chose où je me trouve engagé, qui n’est pas tout entier devant moi » [9]. « Philosopher, pour Gabriel Marcel, dit M. Thibon, commentant ce passage, c’est moins élucider un problème que participer à un mystère » [10]. D’après cette thèse, le problème est public ; il se pose en droit pour tous et de la même manière pour tous (Dieu existe-t-il ? L’homme est-il libre ?) et il concerne la raison et l’intelligence. Le mystère est privé ou tout au plus collectif, n’existant que pour un groupe d’hommes déterminé ; les initiés, en y prenant part, sont modifiés dans leur être plus encore que la [16] connaissance. Mais cette distinction n’est admissible que si le mystère se réfère à une religion révélée ; à part ce trait, on peut dire que toute philosophie tend vers une sagesse et vers une transformation intime de l’homme ; elle aussi, elle nous  « engage » ; la position d’un problème est moins celle d’un « obstacle qui nous barre la route » que l’expression d’une intuition profonde qui se révèle à nous par ce problème lui-même.

Concluons donc, en général, que les problèmes philosophiques n’existent pas en eux-mêmes, séparément, de sorte qu’on les retrouve identiques, mais qu’ils sont des moments dans une pensée philosophique d’ensemble qui contient leur position et leur solution. Il resterait à voir comment cette conception permettrait d’envisager, dans la philosophie, un progrès réel avec qui, au premier abord, elle semble peu compatible.