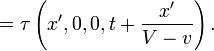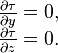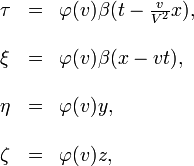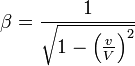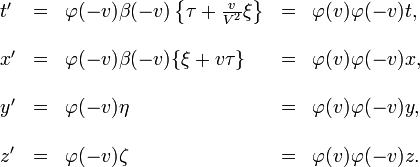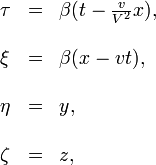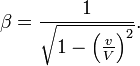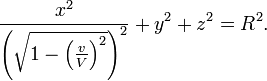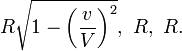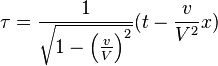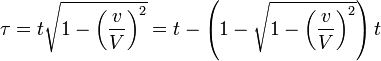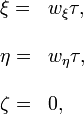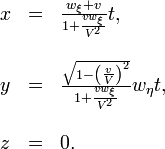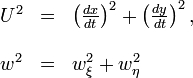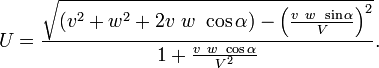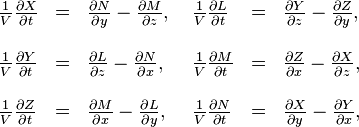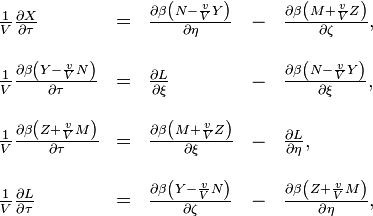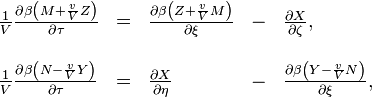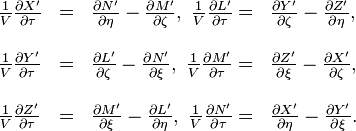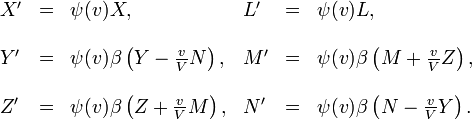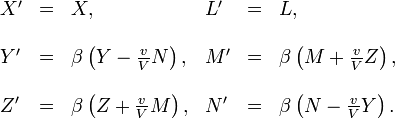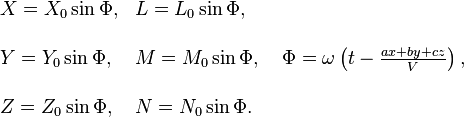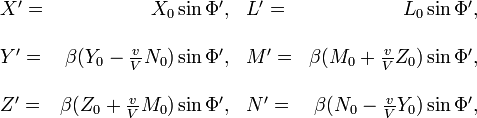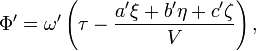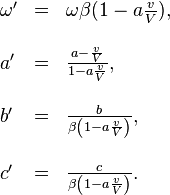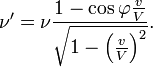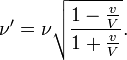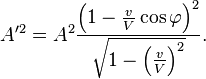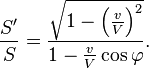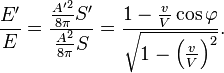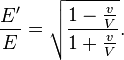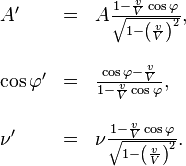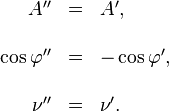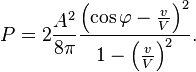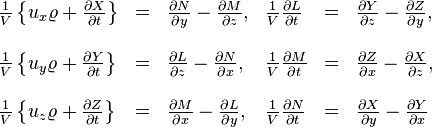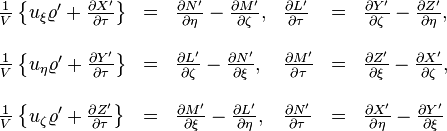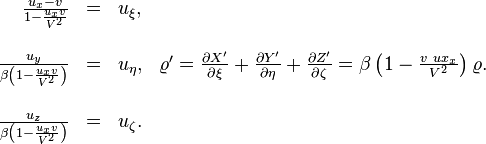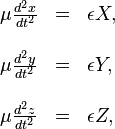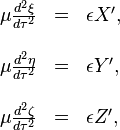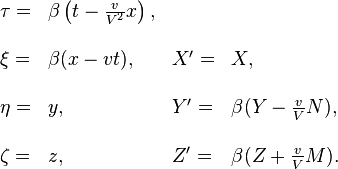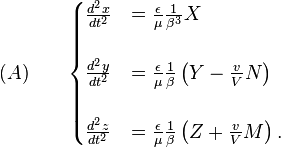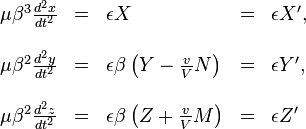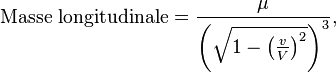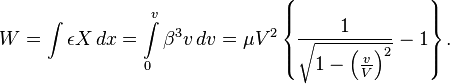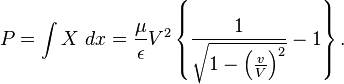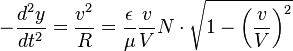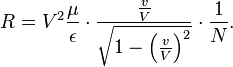Albert Einstein (1905) [2012]
´┐ŻDe l'´┐Żlectrodynamique
des corps en mouvement.´┐Ż
 Cr´┐Żdits
Cr´┐Żdits

Auteur : Albert Einstein
Traducteur de l'allemand vers l'anglais : Meghnad Saha
Relecteurs de la version anglaise : Contributeurs de la Wikisource en anglais (liste accessible en ligne)
Traducteur de l'anglais vers le fran´┐Żais : Cantons-de-l´┐ŻEst
Relecteur de la version fran´┐Żaise : Simon Villeneuve
Pr´┐Żsentation

L'article original d'Albert Einstein en allemand, ´┐Ż´┐ŻZur Elektrodynamik bewegter K´┐Żrper´┐Ż´┐Ż, est publi´┐Ż pour la premi´┐Żre fois en 1905 par la revue de physique Annalen der Physikouvrage 1. Son auteur, Albert Einstein, est mort en 1955. L'article est dans le domaine public aux ´┐Żtats-Unis parce qu'il a ´┐Żt´┐Ż publi´┐Ż avant le 1er janvier 1923. Dans les pays o´┐Ż la dur´┐Że du copyright n'exc´┐Żde pas 50 ans apr´┐Żs le d´┐Żc´┐Żs de son auteur, il est aussi dans le domaine public (c'est le cas au Canada). Finalement, dans certains pays o´┐Ż la r´┐Żgle du terme le plus court s'applique, l'article est aussi dans le domaine public.
L'astrophysicien indien Meghnad Saha a traduit en anglais l'article sous le titre On the Electrodynamics of Moving Bodies, article publi´┐Ż en 1920 par l'universit´┐Ż de Calcutta en Inde. Il est recopi´┐Ż en wikitexte dans la Wikisource en anglaisouvrage 2 (nomm´┐Ż ´┐Ż´┐Żarticle A´┐Ż´┐Ż par la suite pour le distinguer du suivant). Le traducteur, Meghnad Saha, est mort en 1956. L'article est dans le domaine public aux ´┐Żtats-Unis parce qu'il a ´┐Żt´┐Ż publi´┐Ż avant le 1er janvier 1923. Dans les pays o´┐Ż la dur´┐Że du copyright n'exc´┐Żde pas 50 ans apr´┐Żs le d´┐Żc´┐Żs de son auteur, il est aussi dans le domaine public (c'est le cas au Canada). Finalement, dans certains pays o´┐Ż la r´┐Żgle du terme le plus court s'applique, l'article A est aussi dans le domaine public.
La Wikisource en anglais publie un autre article intitul´┐Ż On the Electrodynamics of Moving Bodies (nomm´┐Ż ´┐Ż´┐Żarticle B´┐Ż´┐Ż)ouvrage 3. L'article B est en grande partie une copie de l'article A, le reste est une traduction de l'article d'Albert Einstein. Des contributeurs ont aussi fait des corrections et quelques ajouts, tous publi´┐Żs sous CC BY-SA 3.0.
La traduction en fran´┐Żais qui suit est faite ´┐Ż partir de l'article B. Cette traduction, publi´┐Że en d´┐Żcembre 2012, est publi´┐Że sous la licence Creative Commons CC BY-SA.
En notation moderne, la vitesse de la lumi´┐Żre est indiqu´┐Że par c, mais l'article original comprend quelques ´┐Żquations o´┐Ż ce symbole sert ´┐Ż d'autres fins. Einstein utilise V ´┐Ż la place. Dans la traduction en fran´┐Żais, des modifications ponctuelles sont faites et des informations sont ajout´┐Żes pour faciliter la lecture, la plupart document´┐Żes dans le corps du texte ´┐Ż l'aide de renvois vers des notes du traducteur (NdT).
De l'´┐Żlectrodynamique des corps en mouvement
par Albert Einstein en allemand (1905),
traduit en anglais par Meghnad Saha (1920)
et par la Wikisource en anglais (2011)
´┐Ż
Il est connu que si nous appliquons l'´┐Żlectrodynamique de Maxwell, telle que nous la concevons aujourd'hui, aux corps en mouvement, nous sommes conduits ´┐Ż une asym´┐Żtrie qui ne s'accorde pas avec les ph´┐Żnom´┐Żnes observ´┐Żs. Analysons par exemple l'influence mutuelle d'un aimant et d'un conducteur. Le ph´┐Żnom´┐Żne observ´┐Ż dans ce cas d´┐Żpend uniquement du mouvement relatif du conducteur et de l'aimant, alors que selon les conceptions habituelles, une distinction doit ´┐Żtre ´┐Żtablie entre les cas o´┐Ż l'un ou l'autre des corps est en mouvement. Si par exemple l'aimant se d´┐Żplace et que le conducteur est au repos, alors un champ ´┐Żlectrique d'une certaine ´┐Żnergie appara´┐Żt ´┐Ż proximit´┐Ż de l'aimant, ce qui engendre un courant dans les parties du champ o´┐Ż se trouve un conducteur. Mais si l'aimant est au repos et le conducteur mis en mouvement, aucun champ ´┐Żlectrique n'appara´┐Żt ´┐Ż proximit´┐Ż de l'aimant, mais une force ´┐Żlectromotrice qui ne correspond ´┐Ż aucune ´┐Żnergie en soi est produite dans le conducteur. Elle provoque cependant ´┐Ż´┐Żdans l'hypoth´┐Żse que le mouvement relatif dans les deux cas est le m´┐Żme´┐Ż´┐Ż l'apparition d'un courant ´┐Żlectrique de m´┐Żme intensit´┐Ż et de m´┐Żme direction que la force ´┐Żlectrique, comme la force ´┐Żlectrique dans le premier cas.
Des exemples similaires, tout comme l'essai infructueux de confirmer le mouvement de la Terre relativement au ´┐Ż´┐Żm´┐Żdium de la lumi´┐Żre´┐Ż´┐ŻNdT 1, nous am´┐Żne ´┐Ż la supposition que non seulement en m´┐Żcanique, mais aussi en ´┐Żlectrodynamique, aucune propri´┐Żt´┐Ż des faits observ´┐Żs ne correspond au concept de repos absolu´┐Ż; et que dans tous les syst´┐Żmes de coordonn´┐Żes o´┐Ż les ´┐Żquations de la m´┐Żcanique sont vraies, les ´┐Żquations ´┐Żlectrodynamiques et optiques ´┐Żquivalentes sont ´┐Żgalement vraies, comme il a ´┐Żt´┐Ż d´┐Żj´┐Ż montr´┐Ż par l'approximation au premier ordre des grandeurs. Dans le texte qui suit, nous ´┐Żlevons cette conjecture au rang de postulat (que nous appellerons dor´┐Żnavant ´┐Ż´┐Żprincipe de relativitÚá╗) et introduisons un autre postulat ´┐Ż´┐Żqui au premier regard est incompatible avec le premier´┐Ż´┐Ż que la lumi´┐Żre se propage dans l'espace videNdT 2, ´┐Ż une vitesse V ind´┐Żpendante de l'´┐Żtat de mouvement du corps ´┐Żmetteur. Ces deux postulats suffisent enti´┐Żrement pour former une th´┐Żorie simple et coh´┐Żrente de l'´┐Żlectrodynamique des corps en mouvement ´┐Ż partir de la th´┐Żorie maxwellienne des corps au repos. Il sera d´┐Żmontr´┐Ż que l'introduction d'un ´┐Ż´┐Ż´┐Żther luminif´┐Żre´┐Ż´┐Ż est superflu, puisque selon les conceptions que nous d´┐Żvelopperons, nous n'introduirons ni un ´┐Ż´┐Żespace absolument au repos´┐Ż´┐Ż muni de propri´┐Żt´┐Żs sp´┐Żciales et ni n'associerons un vecteur vitesse ´┐Ż un point o´┐Ż des ph´┐Żnom´┐Żnes ´┐Żlectromagn´┐Żtiques se d´┐Żroulent.
Comme pour toute autre th´┐Żorie ´┐Żlectrodynamique, la th´┐Żorie propos´┐Że s'appuie sur la cin´┐Żmatique des corps rigides. Dans la formulation de toute th´┐Żorie, nous devons composer avec les relations entre les corps rigides (syst´┐Żme de coordonn´┐Żes), les horloges et les ph´┐Żnom´┐Żnes ´┐Żlectromagn´┐Żtiques. Une appr´┐Żciation insuffisante de ces conditions est la cause des probl´┐Żmes auxquels se heurte pr´┐Żsentement l'´┐Żlectrodynamique des corps en mouvement.
´┐Ż
I. Partie cin´┐Żmatique
´┐Ż
´┐Ż 1. D´┐Żfinition de la simultan´┐Żit´┐Ż

Supposons un syst´┐Żme de coordonn´┐Żes dans lequel les ´┐Żquations newtoniennes sont vraies. Pour distinguer ce syst´┐Żme d'un autre qui sera introduit plus tard, et pour rendre cette notion plus claire, nous l'appellerons le ´┐Ż´┐Żsyst´┐Żme stationnaire´┐Ż´┐Ż.
Si un point mat´┐Żriel est au repos dans ce syst´┐Żme de coordonn´┐Żes, alors sa position dans ce syst´┐Żme peut ´┐Żtre trouv´┐Że gr´┐Żce ´┐Ż une r´┐Żgle ´┐Ż mesurerNdT 3 en utilisant des m´┐Żthodes en g´┐Żom´┐Żtrie euclidienne, et exprim´┐Że en coordonn´┐Żes cart´┐Żsiennes.
Si nous voulons d´┐Żcrire le mouvement d'un point mat´┐Żriel, les valeurs de ses coordonn´┐Żes doivent ´┐Żtre exprim´┐Żes en fonction du temps. Il faut toujours garder en t´┐Żte qu'une telle d´┐Żfinition math´┐Żmatique poss´┐Żde un sens physique, seulement si nous avons au pr´┐Żalable une perception claire de ce qu'est le ´┐Ż´┐Żtemps´┐Ż´┐Ż. Nous devons prendre en consid´┐Żration le fait que nos conceptions, o´┐Ż le temps joue un r´┐Żle, portent toujours sur des ´┐Żv´┐Żnements simultan´┐Żs. Par exemple, si nous disons ´┐Ż´┐Żqu'un train arrive ici ´┐Ż 7 heures´┐Ż´┐Ż, cela signifie ´┐Ż´┐Żque la petite aiguille de ma montre qui pointe exactement le 7 et que l'arriv´┐Że du train sont des ´┐Żv´┐Żnements simultan´┐Żs´┐Ż´┐Ż1.
Il peut sembler que toutes les difficult´┐Żs provenant de la d´┐Żfinition du ´┐Ż´┐Żtemps´┐Ż´┐Ż peuvent ´┐Żtre supprim´┐Żes quand, au ´┐Ż´┐Żtemps´┐Ż´┐Ż, nous substituons ´┐Ż´┐Żla position de la petite aiguille de ma montre´┐Ż´┐Ż. Une telle d´┐Żfinition est dans les faits suffisante, quand il est requis de d´┐Żfinir le temps exclusivement ´┐Ż l'endroit o´┐Ż l'horloge se trouve. Mais elle ne suffit plus lorsqu'il s'agit de relier chronologiquement des ´┐Żv´┐Żnements qui ont lieu ´┐Ż des endroits diff´┐Żrents ´┐Ż´┐Żou ce qui revient au m´┐Żme´┐Ż´┐Ż, d'estimer chronologiquement l'occurrence d'´┐Żv´┐Żnements qui surviennent ´┐Ż des endroits ´┐Żloign´┐Żs de l'horloge.
Cependant, pour estimer chronologiquement les ´┐Żv´┐Żnements, nous pouvons obtenir satisfaction en supposant qu'un observateur, plac´┐Ż ´┐Ż l'origine du syst´┐Żme de coordonn´┐Żes avec l'horloge, associe un signal lumineux ´┐Ż´┐Żt´┐Żmoignant de l'´┐Żv´┐Żnement ´┐Ż estimer et du rayon lumineux qui vient ´┐Ż lui ´┐Ż travers l'espace´┐Ż´┐Ż ´┐Ż la position correspondante des aiguilles de l'horloge. Cependant, une telle association a un d´┐Żfaut´┐Ż: elle d´┐Żpend de la position de l'observateur qui observe l'horloge, comme l'exp´┐Żrience nous le dicte. Nous pouvons obtenir un r´┐Żsultat beaucoup plus pratique de la fa´┐Żon suivante.
Si un observateur est plac´┐Ż en A avec une horloge, il peut assigner un temps aux ´┐Żv´┐Żnements ´┐Ż proximit´┐Ż de A en observant la position des aiguilles de l'horloge, qui sont simultan´┐Żes avec l'´┐Żv´┐Żnement. Si une horloge est aussi plac´┐Że en B ´┐Ż´┐Żnous ajoutons que cette horloge est de m´┐Żme construction que celle en A´┐Ż´┐Ż, alors un observateur en B peut chronologiquement estimer les ´┐Żv´┐Żnements qui surviennent dans le voisinage de B. Mais sans conventions pr´┐Żalables, il est impossible de comparer chronologiquement les ´┐Żv´┐Żnements en B aux ´┐Żv´┐Żnements en A. Nous avons jusqu'´┐Ż maintenant un ´┐Ż´┐Żtemps A´┐Ż´┐Ż et un ´┐Ż´┐Żtemps B´┐Ż´┐Ż, mais aucun ´┐Ż´┐Żtemps´┐Ż´┐Ż commun ´┐Ż A et B. Ce dernier temps (c'est-´┐Ż-dire le temps commun) peut ´┐Żtre d´┐Żfini, si nous posons par d´┐Żfinition que le ´┐Ż´┐Żtemps´┐Ż´┐Ż requis par la lumi´┐Żre pour aller de A ´┐Ż B est ´┐Żquivalent au ´┐Ż´┐Żtemps´┐Ż´┐Ż pris par la lumi´┐Żre pour aller de B ´┐Ż A. Par exemple, un rayon lumineux part de A au ´┐Ż´┐Żtemps A´┐Ż´┐Ż, tA, en direction de B, est r´┐Żfl´┐Żchi de B au ´┐Ż´┐Żtemps B´┐Ż´┐Ż, tB, et revient ´┐Ż A au ´┐Ż´┐Żtemps A´┐Ż´┐Ż, t'A. Par d´┐Żfinition, les deux horloges sont synchronis´┐Żes si
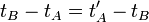 .
.
Nous supposons que cette d´┐Żfinition du synchronisme est possible sans causer d'incoh´┐Żrence, peu importe le nombre de points. En cons´┐Żquence les relations suivantes sont vraies´┐Ż:
1. Si l'horloge en B est synchronis´┐Że avec l'horloge en A, alors l'horloge en A est synchronis´┐Że avec l'horloge en B.
2. Si l'horloge en A est synchronis´┐Że ´┐Ż la fois avec l'horloge en B et avec l'horloge en C, alors les horloges en B et C sont synchronis´┐Żes.
Donc, ´┐Ż l'aide de certaines exp´┐Żriences physiques (de pens´┐Że), nous avons ´┐Żtabli ce que nous entendons lorsque nous parlons d'horloges au repos ´┐Ż diff´┐Żrents endroits, et synchronis´┐Żes les unes avec les autres´┐Ż; et nous avons par cons´┐Żquent ´┐Żtabli une d´┐Żfinition de la ´┐Ż´┐Żsimultan´┐ŻitÚá╗ et du ´┐Ż´┐Żtemps´┐Ż´┐Ż. Le ´┐Ż´┐Żtemps´┐Ż´┐Ż d'un ´┐Żv´┐Żnement est l'indication simultan´┐Że d'une horloge au repos situ´┐Że ´┐Ż l'endroit de l'´┐Żv´┐Żnement, qui est synchronis´┐Że avec une certaine horloge au repos dans tous les cas de d´┐Żtermination du temps.
En accord avec l'exp´┐Żrience, nous ferons donc l'hypoth´┐Żse que la grandeur

est une constante universelle (la vitesse de la lumi´┐Żre dans l'espace vide).
Nous venons de d´┐Żfinir le temps ´┐Ż l'aide d'une horloge au repos dans un syst´┐Żme stationnaire. Puisqu'il existe en propre dans un syst´┐Żme stationnaire, nous appelons le temps ainsi d´┐Żfini ´┐Ż´┐Żtemps du syst´┐Żme stationnaire´┐Ż´┐Ż.
´┐Ż
´┐Ż 2. Sur la relativit´┐Ż des longueurs et des temps

Les r´┐Żflexions suivantes s'appuient sur le principe de relativit´┐Ż et sur le principe de la constance de la vitesse de la lumi´┐Żre, les deux que nous d´┐Żfinissons comme suit´┐Ż:
1. Les lois selon lesquelles l'´┐Żtat des syst´┐Żmes physiques se transforme sont ind´┐Żpendantes de la fa´┐Żon que ces changements sont rapport´┐Żs dans deux syst´┐Żmes de coordonn´┐Żes (syst´┐Żmes qui sont en mouvement rectiligne uniformeNdT 4 l'un par rapport ´┐Ż l'autre).
2. Chaque rayon lumineux se d´┐Żplace dans un syst´┐Żme de coordonn´┐Żes ´┐Ż´┐Żstationnaire´┐Ż´┐Ż ´┐Ż la m´┐Żme vitesse V, la vitesse ´┐Żtant ind´┐Żpendante de la condition que ce rayon lumineux soit ´┐Żmis par un corps au repos ou en mouvement. Donc,

o´┐Ż ´┐Ż´┐Żintervalle de temps´┐Ż´┐Ż doit ´┐Żtre compris tel que d´┐Żfini au ´┐Ż 1.
Soit une tige rigide au repos´┐Ż; elle est d'une longueur l quand elle est mesur´┐Że par une r´┐Żgle au repos. Nous supposons que l'axe de la tige se confond avec l'axe des x du syst´┐Żme stationnaire. Imprimons ´┐Ż la tige une vitesse uniforme v, parall´┐Żle ´┐Ż l'axe des x et dans la direction des x croissants. Quelle est la longueur de la longueur de la tige en mouvement´┐Ż? Elle peut ´┐Żtre obtenue de deux fa´┐Żons´┐Ż:
a) L'observateur pourvu de la r´┐Żgle ´┐Ż mesurer se d´┐Żplace avec la tige ´┐Ż mesurer et mesure sa longueur en superposant la r´┐Żgle sur la tige, comme si l'observateur, la r´┐Żgle ´┐Ż mesurer et la tige sont au repos.
b) L'observateur d´┐Żtermine ´┐Ż quels points du syst´┐Żme stationnaire se trouvent les extr´┐Żmit´┐Żs de la tige ´┐Ż mesurer au temps t, se servant des horloges plac´┐Żes dans le syst´┐Żme stationnaire (les horloges ´┐Żtant synchronis´┐Żes comme d´┐Żcrit au ´┐Ż 1). La distance entre ces deux points, mesur´┐Że par la m´┐Żme r´┐Żgle ´┐Ż mesurer quand elle ´┐Żtait au repos, est aussi une longueur, que nous appelons la ´┐Ż´┐Żlongueur de la tige´┐Ż´┐Ż.
Selon le principe de relativit´┐Ż, la longueur trouv´┐Że par l'op´┐Żration a), que nous appelons la ´┐Ż´┐Żlongueur de la tige dans le syst´┐Żme en mouvement´┐Ż´┐Ż, est ´┐Żgale ´┐Ż la longueur l de la tige dans le syst´┐Żme stationnaire.
La longueur trouv´┐Że par l'op´┐Żration b) peut ´┐Żtre appel´┐Że la ´┐Ż´┐Żlongueur de la tige (en mouvement) dans le syst´┐Żme stationnaire´┐Ż´┐Ż. Cette longueur est ´┐Ż calculer en s'appuyant sur nos deux principes, et nous d´┐Żcouvrirons qu'elle diff´┐Żre de l.
Dans la cin´┐Żmatique g´┐Żn´┐Żralement utilis´┐Że, il est implicitement suppos´┐Ż que les longueurs d´┐Żfinies par ces deux op´┐Żrations sont ´┐Żgales ou, dit autrement, qu'´┐Ż un moment donn´┐Ż t, une tige rigide en mouvement est g´┐Żom´┐Żtriquement rempla´┐Żable par un m´┐Żme corps, quand il est au repos ´┐Ż un endroit pr´┐Żcis.
Supposons de plus que deux horloges synchronis´┐Żes avec des horloges dans le syst´┐Żme stationnaire sont fix´┐Żes aux extr´┐Żmit´┐Żs A et B d'une tige, c'est-´┐Ż-dire que les temps des horloges correspondent aux ´┐Ż´┐Żtemps du syst´┐Żme stationnaire´┐Ż´┐Ż aux points o´┐Ż elles arrivent´┐Ż; ces horloges sont donc ´┐Ż´┐Żsynchronis´┐Żes dans le syst´┐Żme stationnaire´┐Ż´┐Ż.
Imaginons encore qu'il y a deux observateurs aupr´┐Żs des deux horloges qui se d´┐Żplacent avec elles, et que ces observateurs appliquent le crit´┐Żre de synchronisme du ´┐Ż 1 aux deux horloges. Au temps2 tA, un rayon lumineux va de A, est r´┐Żfl´┐Żchi par B au temps tB et arrive ´┐Ż A au temps t'A. Prenant en compte le principe de la constance de la vitesse de la lumi´┐Żre, nous avons
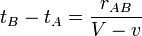 ,
,
et
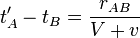 ,
,
o´┐Ż rAB est la longueur de la tige en mouvement, mesur´┐Że dans le syst´┐Żme stationnaire. En cons´┐Żquence, les observateurs qui se d´┐Żplacent avec la tige en mouvement n'affirmeront pas que les horloges sont synchronis´┐Żes, m´┐Żme si les observateurs dans le syst´┐Żme stationnaire t´┐Żmoigneront que les horloges sont synchronis´┐Żes.
Nous en concluons que nous ne pouvons pas attacher une signification absolue au concept de simultan´┐Żit´┐Ż. D´┐Żs lors, deux ´┐Żv´┐Żnements qui sont simultan´┐Żs lorsque observ´┐Żs d'un syst´┐Żme ne seront pas simultan´┐Żs lorsque observ´┐Żs d'un syst´┐Żme en mouvement relativement au premier.
´┐Ż
´┐Ż 3. Th´┐Żorie de la transformation des coordonn´┐Żes
et du temps d'un syst´┐Żme stationnaire ´┐Ż un autre
en mouvement relatif uniforme comparativement
au premier

Pla´┐Żons, dans le syst´┐Żme ´┐Ż´┐Żstationnaire´┐Ż´┐Ż, deux syst´┐Żmes de coordonn´┐Żes, c'est-´┐Ż-dire deux s´┐Żries de trois axes rigides (mutuellement perpendiculaires) tous issus d'un pointNdT 5. Faisons co´┐Żncider l'axe des x de chacun des syst´┐Żmes et mettons en parall´┐Żle les axes des y et des z. Soit une r´┐Żgle rigide et un certain nombre d'horloges dans chaque syst´┐Żme, les tiges et les horloges dans chacun ´┐Żtant identiques.
Soit un point initial de l'un des syst´┐Żmes (k) anim´┐Ż d'une vitesse (constante) v selon l'axe des x dans la direction des x croissants de l'autre syst´┐Żme, un syst´┐Żme stationnaire (K), et la vitesse ´┐Żtant aussi communiqu´┐Że aux axes, aux tiges et aux horloges dans le syst´┐Żme. N'importe quel temps t du syst´┐Żme stationnaire K correspond ´┐Ż une position certaine des axes du syst´┐Żme en mouvement. Pour des raisons de sym´┐Żtrie, nous pouvons affirmer que le mouvement de k est tel que les axes du syst´┐Żme en mouvement au temps t (par t, nous entendons le temps dans le syst´┐Żme stationnaire) sont parall´┐Żles aux axes du syst´┐Żme stationnaire.
Supposons que l'espace est mesur´┐Ż par la r´┐Żgle immobile plac´┐Że dans le syst´┐Żme stationnaire K, tout comme par la r´┐Żgle en mouvement plac´┐Że dans le syst´┐Żme en mouvement k, nous avons donc les coordonn´┐Żes x, y, z et ξ, η, ζ, respectivement. De plus, mesurons le temps t ´┐Ż chaque point du syst´┐Żme stationnaire gr´┐Żce aux horloges qui sont plac´┐Żes dans le syst´┐Żme stationnaire, ´┐Ż l'aide de la m´┐Żthode des signaux lumineux d´┐Żcrite au ´┐Ż 1. Soit aussi le temps τ dans le syst´┐Żme en mouvement qui est connu pour chaque point du syst´┐Żme en mouvement (dans lequel se trouvent des horloges qui sont au repos dans le syst´┐Żme en mouvement), gr´┐Żce ´┐Ż la m´┐Żthode des signaux lumineux entre ces points (positions o´┐Ż se trouvent des horloges) d´┐Żcrit au ´┐Ż 1.
Pour chacun des ensembles de valeurs x, y, z, t qui indique compl´┐Żtement la position et le temps de l'´┐Żv´┐Żnement dans le syst´┐Żme stationnaire, il existe un ensemble de valeurs ξ, η, ζ, τ dans le syst´┐Żme k. Maintenant, le probl´┐Żme est de trouver le syst´┐Żme d'´┐Żquations qui relie ces valeurs.
Premi´┐Żrement, il est ´┐Żvident que, en s'appuyant sur la propri´┐Żt´┐Ż d'homog´┐Żn´┐Żit´┐Ż que nous attribuons au temps et ´┐Ż l'espace, les ´┐Żquations doivent ´┐Żtre lin´┐Żaires.
Si nous posons x' = x - vt, alors il est ´┐Żvident que pour un point au repos dans le syst´┐Żme k, il y a un syst´┐Żme de valeurs x', y, z ind´┐Żpendant du temps. Premi´┐Żrement, trouvons τ comme fonction de x', y, z, t. ´┐Ż cet effet, nous devons exprimer en ´┐Żquations le fait que τ n'est nul autre que le temps donn´┐Ż par les horloges au repos dans le syst´┐Żme k qui doivent ´┐Żtre synchronis´┐Żes selon la m´┐Żthode d´┐Żcrite au ´┐Ż 1.
Soit un rayon lumineux envoy´┐Ż au temps τ0 de l'origine du syst´┐Żme k selon l'axe des x dans la direction des x croissants et qui est r´┐Żfl´┐Żchi de cet endroit au temps τ1 vers l'origine des coordonn´┐Żes, o´┐Ż il arrive au temps τ2. Alors, nous avons
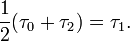
Si nous introduisons comme condition que τ est une fonction des coordonn´┐Żes, et appliquons le principe de la constance de la vitesse de la lumi´┐Żre dans le syst´┐Żme stationnaire, nous avons
![\frac{1}{2}\left[\tau(0,0,0,t)+\tau\left(0,0,0,\left\{ t+\frac{x'}{V-v}+\frac{x'}{V+v}\right\} \right)\right]](Electrodynamique_files/image007.gif)
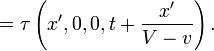
Il s'ensuit donc, lorsque x' est infiniment petit´┐Ż:
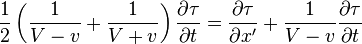
ou
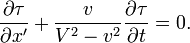
Notons qu'au lieu de l'origine des coordonn´┐Żes, nous pourrions choisir n'importe quel autre point comme point de d´┐Żpart pour les rayons lumineux, et en cons´┐Żquence l'´┐Żquation ci-dessus est vraie pour toutes les valeurs de x', y, z.
Une approche semblable appliqu´┐Że aux axes des y et des z donne, quand nous prenons en compte le fait que la lumi´┐Żre se propage toujours le long de ces axes ´┐Ż une vitesse
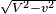 lorsque observ´┐Że depuis le syst´┐Żme stationnaire, ces ´┐Żquations´┐Ż:
lorsque observ´┐Że depuis le syst´┐Żme stationnaire, ces ´┐Żquations´┐Ż:
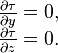
Puisque
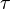 est une fonction lin´┐Żaire, il suit de ces ´┐Żquations que
est une fonction lin´┐Żaire, il suit de ces ´┐Żquations que
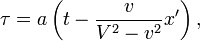
o´┐Ż a est une fonction inconnue φ(v) et pour des raisons de concision, il est fait l'hypoth´┐Żse qu'´┐Ż l'origine de k, t = 0 lorsque τ = 0.
´┐Ż l'aide de ces r´┐Żsultats, il est facile d'obtenir les grandeurs ξ, η, ζ, si nous exprimons (en ´┐Żquations) le fait que la lumi´┐Żre (lorsque mesur´┐Że dans le syst´┐Żme en mouvement) se propage toujours ´┐Ż la vitesse constante V (tel que requis par le principe de la constance de la vitesse de la lumi´┐Żre et le principe de la relativit´┐Ż). Pour un rayon envoy´┐Ż dans la direction des ξ croissants au temps τ = 0, nous avons
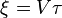
ou
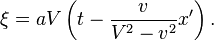
Cependant, le rayon lumineux se d´┐Żplace relativement ´┐Ż l'origine de k ´┐Ż une vitesse V-v, mesur´┐Że dans le syst´┐Żme stationnaire. En cons´┐Żquence, nous obtenons
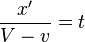 .
.
Rempla´┐Żant ces valeurs de t dans l'´┐Żquation de ξ, nous obtenons
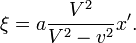
D'une fa´┐Żon analogue, si les rayon lumineux se d´┐Żplacent selon les deux autres axes, nous avons
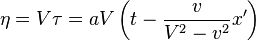
o´┐Ż
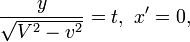
et donc
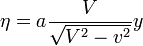
et
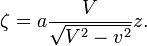
Si pour x', nous substituons sa valeur, nous obtenons
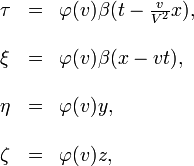
o´┐Ż
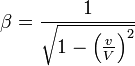
et φ est encore une fonction inconnue de v. Si nous ne faisons aucune hypoth´┐Żse sur la position initiale du syst´┐Żme en mouvement et sur le point sans dimension τ, alors une constante additive doit ´┐Żtre ajout´┐Że du c´┐Żt´┐Ż droit de l'´┐Żquation.
Nous devons d´┐Żmontrer que tout rayon lumineux se d´┐Żplace dans le syst´┐Żme en mouvement ´┐Ż une vitesse V (telle que mesur´┐Że dans le syst´┐Żme en mouvement) si, comme nous en avons d´┐Żj´┐Ż fait l'hypoth´┐Żse, V est aussi la vitesse dans le syst´┐Żme stationnaire. En effet, nous n'avons pas encore pr´┐Żsent´┐Ż une quelconque preuve que le principe de la constance de la vitesse de la lumi´┐Żre est compatible avec le principe de relativit´┐Ż.
Au temps τ = t = 0, soit une onde sph´┐Żrique ´┐Żmise depuis l'origine commune des deux syst´┐Żmes de coordonn´┐Żes, onde qui se propage ´┐Ż une vitesse V dans le syst´┐Żme K. Si (x, y, z) est un point atteint par l'onde, alors
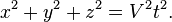
´┐Ż l'aide de nos ´┐Żquations de transformations, faisons la transformation de cette ´┐Żquation. Par un simple calcul nous avons
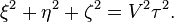
En cons´┐Żquence, l'onde se propage dans le syst´┐Żme en mouvement ´┐Ż la m´┐Żme vitesse V, comme une onde sph´┐Żrique. Donc, nous avons d´┐Żmontr´┐Ż que les deux principes sont mutuellement compatibles.
Par les transformations, nous avons obtenu une fonction ind´┐Żtermin´┐Że φ de v, que nous allons maintenant d´┐Żterminer.
Dans ce but, introduisons un troisi´┐Żme syst´┐Żme de coordonn´┐Żes K' , qui est en mouvement relatif par rapport au syst´┐Żme k, le mouvement ´┐Żtant parall´┐Żle ´┐Ż l'axe des Ξ de fa´┐Żon ´┐Ż ce que la vitesse de l'origine soit -v par rapport ´┐Ż l'axe des Ξ. Au temps t = 0, toutes les coordonn´┐Żes des points initiaux co´┐Żncident, et pour t = x = y = z = 0, le temps t' du syst´┐Żme K' = 0. Si nous posons que x', y', z' sont les coordonn´┐Żes mesur´┐Żes dans le syst´┐Żme K' , alors par une double application des ´┐Żquations de transformations, nous obtenons
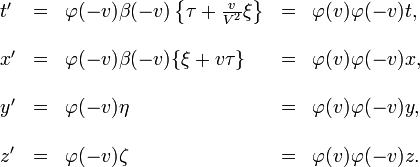
Puisque les relations entre x', y', z' et x, y, z ne comprennent pas explicitement le temps t, K et K' sont donc relativement au repos. Il appara´┐Żt clairement que la transformation de K ´┐Ż K' doit ´┐Żtre identique. D'o´┐Ż
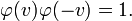
Nous sommes pr´┐Żt ´┐Ż calculer φ(v). Portons notre attention sur la partie de l'axe des y du syst´┐Żme k entre ξ = 0, η = 0, ζ = 0 et ξ = 0, η = 1, ζ = 0. Couvrons cette partie de l'axe des y avec une tige qui se d´┐Żplace ´┐Ż une vitesse v relativement au syst´┐Żme K et perpendiculairement ´┐Ż son axe. Les extr´┐Żmit´┐Żs de la tige ont donc comme coordonn´┐Żes dans K´┐Ż:
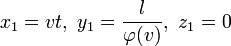
et
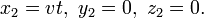
En cons´┐Żquence, la longueur de la tige mesur´┐Że dans le syst´┐Żme K est l / φ(v). Donc, la signification de φ est connue. Pour des raisons de sym´┐Żtrie, il est maintenant ´┐Żvident que la longueur (mesur´┐Że dans le syst´┐Żme stationnaire) d'une certaine tige qui se d´┐Żplace perpendiculairement ´┐Ż son axe, peut seulement d´┐Żpendre de sa vitesse, mais pas de la direction et du sens du mouvement. Donc, la longueur de la tige en mouvement, telle que mesur´┐Że dans le syst´┐Żme stationnaire, ne change pas si v est remplac´┐Ż par -v. Nous avons donc´┐Ż:
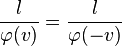
ou
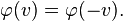
De ceci et des relations trouv´┐Żes plus haut, il suit que φ(v) = 1. Donc, les ´┐Żquations de transformations deviennent´┐Ż:
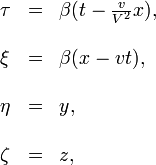
o´┐Ż
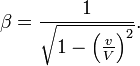
´┐Ż
´┐Ż 4. La signification physique des ´┐Żquations obtenues
pour les corps rigides et les horloges en mouvement

Supposons une sph´┐Żre rigide´┐Ż3 de rayon R qui est au repos relativement au syst´┐Żme k et dont le centre co´┐Żncide avec l'origine de K, alors l'´┐Żquation de la surface de cette sph´┐Żre, qui se d´┐Żplace ´┐Ż une vitesse v relativement ´┐Ż K, est´┐Ż:
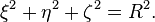
Au temps t = 0, l'´┐Żquation de cette surface s'exprime en fonction de x, y, z par
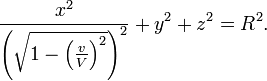
Un corps rigide, qui montre la forme d'une sph´┐Żre quand mesur´┐Ż dans un syst´┐Żme stationnaire, a en cons´┐Żquence dans des conditions de mouvement ´┐Ż´┐Żlorsqu'observ´┐Ż depuis le syst´┐Żme stationnaire´┐Ż´┐Ż, la forme d'un ellipso´┐Żde de r´┐Żvolution dont les demi-axes mesurent
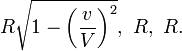
Alors que les dimensions en y et z de la sph´┐Żre (ou de n'importe quel autre solide) ne semblent pas modifi´┐Żes par le mouvement, la dimension en x est raccourcie selon le rapport
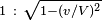 ´┐Ż; le raccourcissement est d'autant plus grand que la vitesse v est grande. Pour v = V, tous les corps en mouvement, lorsqu'observ´┐Żs depuis un syst´┐Żme stationnaire, se r´┐Żduisent ´┐Ż des plans. Pour une vitesse supraluminique, nos propositions sont d´┐Żnu´┐Żes de sens. Par ailleurs, dans les observations qui suivent, nous d´┐Żcouvrirons que la vitesse de la lumi´┐Żre joue le r´┐Żle physique d'une vitesse infiniment grande.
´┐Ż; le raccourcissement est d'autant plus grand que la vitesse v est grande. Pour v = V, tous les corps en mouvement, lorsqu'observ´┐Żs depuis un syst´┐Żme stationnaire, se r´┐Żduisent ´┐Ż des plans. Pour une vitesse supraluminique, nos propositions sont d´┐Żnu´┐Żes de sens. Par ailleurs, dans les observations qui suivent, nous d´┐Żcouvrirons que la vitesse de la lumi´┐Żre joue le r´┐Żle physique d'une vitesse infiniment grande.
Il est ´┐Żvident que des r´┐Żsultats semblables sont vrais pour des corps au repos dans un syst´┐Żme stationnaire lorsqu'ils sont observ´┐Żs depuis un syst´┐Żme en mouvement rectiligne uniforme.
Soit une horloge immobile dans le syst´┐Żme stationnaire qui donne le temps t, et qui donne le temps τ lorsqu'immobile dans un syst´┐Żme en mouvement. Supposons qu'elle se trouve ´┐Ż l'origine du syst´┐Żme en mouvement k et r´┐Żgl´┐Że pour donner le temps τ. ´┐Ż quelle cadence avance cette horloge, lorsqu'observ´┐Że du syst´┐Żme stationnaire´┐Ż?
´┐Ż partir des grandeurs x, t et τ, qui r´┐Żf´┐Żrent ´┐Ż l'endroit de cette horloge, les ´┐Żquations sont donn´┐Żes par
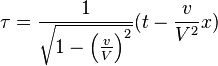
et
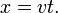
D'o´┐Ż
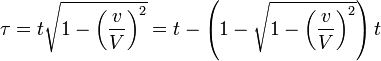 .
.
Donc, l'horloge retarde de
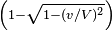 secondes (lorsqu'observ´┐Że du syst´┐Żme stationnaire) par seconde ou, en n´┐Żgligeant les approximations du quatri´┐Żme ordre et sup´┐Żrieurs,
secondes (lorsqu'observ´┐Że du syst´┐Żme stationnaire) par seconde ou, en n´┐Żgligeant les approximations du quatri´┐Żme ordre et sup´┐Żrieurs,
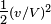 secondes.
secondes.
De ceci d´┐Żcoulent des cons´┐Żquences remarquables. Supposons qu'en deux points A et B de K, lorsqu'observ´┐Żes depuis le syst´┐Żme stationnaire, se trouvent deux horloges synchronis´┐Żes. Supposons que l'horloge en A est mise en mouvement ´┐Ż la vitesse v sur une ligne qui rejoint B, alors lorsqu'elle arrive ´┐Ż B, les deux ne seront plus synchronis´┐Żes, mais l'horloge qui s'est d´┐Żplac´┐Że de A ´┐Ż B aura un retard sur l'horloge toujours demeur´┐Że en B de la quantit´┐Ż
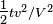 secondes (en n´┐Żgligeant les approximations du quatri´┐Żme ordre et sup´┐Żrieurs), o´┐Ż t est le temps pris pour accomplir le d´┐Żplacement de A ´┐Ż B.
secondes (en n´┐Żgligeant les approximations du quatri´┐Żme ordre et sup´┐Żrieurs), o´┐Ż t est le temps pris pour accomplir le d´┐Żplacement de A ´┐Ż B.
Nous voyons imm´┐Żdiatement que ce r´┐Żsultat est ´┐Żgalement vrai quand l'horloge se d´┐Żplace de A ´┐Ż B en suivant une ligne polygonale, et aussi quand A et B co´┐Żncident.
Si nous faisons l'hypoth´┐Żse que le r´┐Żsultat obtenu pour une ligne polygonale est ´┐Żgalement vrai pour une ligne courbe, nous obtenons le th´┐Żor´┐Żme suivant´┐Ż: Si ´┐Ż A, il y a deux horloges synchronis´┐Żes et si nous d´┐Żpla´┐Żons l'une d'elles ´┐Ż une vitesse constante selon une courbe ferm´┐Że qui revient ´┐Ż A, le d´┐Żplacement ´┐Żtant compl´┐Żt´┐Ż en t secondes, alors ´┐Ż son arriv´┐Że ´┐Ż A, cette derni´┐Żre retardera de
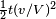 secondes sur l'horloge immobile. En s'appuyant sur ce r´┐Żsultat, nous concluons qu'une horloge ´┐Ż balancier plac´┐Że ´┐Ż l'´┐Żquateur doit ´┐Żtre plus lente par une tr´┐Żs petite quantit´┐Ż qu'une autre identique plac´┐Że ´┐Ż l'un des p´┐Żles, les autres conditions ´┐Żtant identiques.
secondes sur l'horloge immobile. En s'appuyant sur ce r´┐Żsultat, nous concluons qu'une horloge ´┐Ż balancier plac´┐Że ´┐Ż l'´┐Żquateur doit ´┐Żtre plus lente par une tr´┐Żs petite quantit´┐Ż qu'une autre identique plac´┐Że ´┐Ż l'un des p´┐Żles, les autres conditions ´┐Żtant identiques.
´┐Ż
´┐Ż 5. Th´┐Żor´┐Żme d'addition des vitesses

Soit un point en mouvement dans le syst´┐Żme k (qui se d´┐Żplace ´┐Ż une vitesse v parall´┐Żlement ´┐Ż l'axe des x du syst´┐Żme K) qui respecte les ´┐Żquations
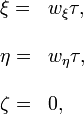
o´┐Ż wξ et wη sont des constantes.
Trouvons le mouvement du point relativement au syst´┐Żme K. Si nous ins´┐Żrons les grandeurs x, y, z, t dans les ´┐Żquations du mouvement en utilisant les ´┐Żquations de transformation du ´┐Ż 3, nous obtenons
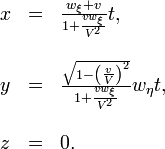
La r´┐Żgle du parall´┐Żlogramme pour les vitesses est seulement vraie pour l'approximation au premier ordre. Nous ´┐Żcrivons donc
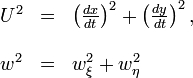
et
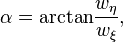
c'est-´┐Ż-dire que α est ´┐Żgal ´┐Ż l'angle entre les vitesses v et w. Alors, apr´┐Żs un simple calcul, nous avons
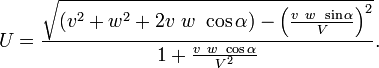
On observe que v et w sont introduits dans l'expression de la vitesse de fa´┐Żon sym´┐Żtrique. Si w est aussi dans la direction de l'axe des x du syst´┐Żme en mouvement, nous avons
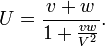
De cette ´┐Żgalit´┐Ż, il d´┐Żcoule que la combinaison de deux vitesses, chacune ´┐Żtant plus petite que V, donne une vitesse toujours plus petite que V. Si nous posons v = V - ϰ et w = V-λ, o´┐Ż ϰ et λ sont chacune positive et plus petite que V, alors
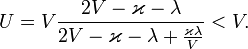
Il est ´┐Żgalement ´┐Żvident que la vitesse de la lumi´┐Żre V ne peut ´┐Żtre modifi´┐Że en lui ajoutant une valeur plus petite. Dans ce cas, nous obtenons
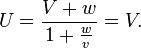
Nous avons d´┐Żduit la formule pour U dans le cas o´┐Ż v et w sont dans la m´┐Żme direction´┐Ż; elle peut aussi ´┐Żtre calcul´┐Że en combinant deux transformations selon la section ´┐Ż 3. Si en plus des syst´┐Żmes K et k du ´┐Ż 3, nous introduisons un troisi´┐Żme syst´┐Żme k' (qui se d´┐Żplace parall´┐Żlement ´┐Ż k), dans lequel le point initial se d´┐Żplace parall´┐Żlement ´┐Ż l'axe des Ξ ´┐Ż une vitesse w, alors entre la grandeurs x, y, z, t et les grandeurs correspondantes de k' , nous obtenons un syst´┐Żme d'´┐Żquations diff´┐Żrent des ´┐Żquations au ´┐Ż 3, en substituant ´┐Ż v cette grandeur
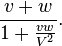
Nous observons qu'une telle transformation parall´┐Żle forme (comme il se doit) un groupe.
Nous avons d´┐Żduit la cin´┐Żmatique qui correspond ´┐Ż nos deux principes fondamentaux pour les lois qui nous sont n´┐Żcessaires, et nous passons maintenant ´┐Ż leur application en ´┐Żlectrodynamique.
´┐Ż
II. Partie ´┐Żlectrodynamique
´┐Ż
´┐Ż 6. Transformation des ´┐Żquations de Maxwell-Hertz
dans un espace vide. Sur la nature de la force ´┐Żlectromotrice
induite par le mouvement dans un champ magn´┐Żtique

Les ´┐Żquations de Maxwell-Hertz dans un espace vide devraient ´┐Żtre vraies dans un syst´┐Żme stationnaire K, d'o´┐Ż
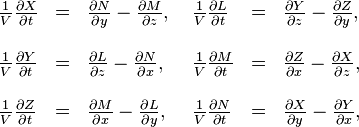
o´┐Ż (X, Y, Z) est le vecteur de la force ´┐Żlectrique et (L, M, N), de la force magn´┐Żtique.
Si nous appliquons les transformations du ´┐Ż 3 ´┐Ż ces ´┐Żquations et si nous ramenons les processus ´┐Żlectromagn´┐Żtiques au syst´┐Żme de coordonn´┐Żes (introduit ´┐Ż cet endroit) se d´┐Żpla´┐Żant ´┐Ż une vitesse v, nous avons
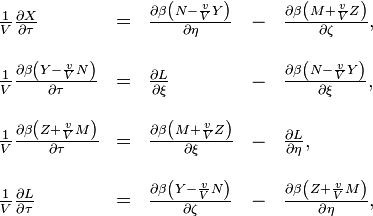
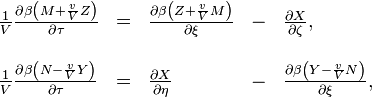
o´┐Ż
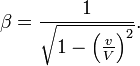
Le principe de relativit´┐Ż exige que les ´┐Żquations de Maxwell-Hertz dans un espace vide soient vraies dans le syst´┐Żme k, si elles sont vraies dans le syst´┐Żme K, c'est-´┐Ż-dire que, pour les vecteurs des forces ´┐Żlectriques et magn´┐Żtiques ((X', Y', Z') et (L', M', N')) qui influencent les masses ´┐Żlectriques et magn´┐Żtiques du syst´┐Żme en mouvement k, qui sont d´┐Żfinies par leurs r´┐Żactions pond´┐Żromotrices, les ´┐Żquations sont vraies,
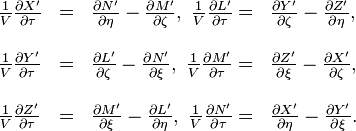
´┐Żvidemment, les deux syst´┐Żmes d'´┐Żquations (2) et (3) d´┐Żvelopp´┐Żs pour le syst´┐Żme k devraient exprimer les m´┐Żmes choses, puisque ces deux syst´┐Żmes sont ´┐Żquivalents aux ´┐Żquations de Maxwell-Hertz du syst´┐Żme K. Puisque les deux syst´┐Żmes d'´┐Żquations (2) et (3) co´┐Żncident jusqu'aux symboles repr´┐Żsentant les vecteurs, il suit que les fonctions apparaissant aux places correspondantes co´┐Żncident au facteur ψ(v) pr´┐Żs, qui d´┐Żpend peut-´┐Żtre de v et est ind´┐Żpendant de ξ, η, ζ, τ. D'o´┐Ż les relations,
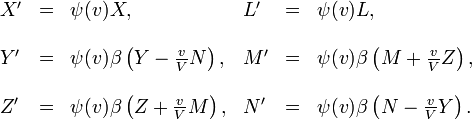
Maintenant, si la r´┐Żciproque de ce syst´┐Żme d'´┐Żquations est form´┐Że, premi´┐Żrement en r´┐Żsolvant les ´┐Żquations que nous venons d'obtenir, deuxi´┐Żmement en appliquant les ´┐Żquations ´┐Ż la transformation inverse (de k ´┐Ż K), qui a comme caract´┐Żristique la vitesse -v, il suit, en sachant que les deux syst´┐Żmes d'´┐Żquations ainsi calcul´┐Żs doivent ´┐Żtre identiques´┐Ż:
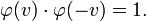
Toujours pour des raisons de sym´┐Żtrie4
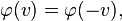
d'o´┐Ż
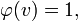
et nos ´┐Żquations prennent la forme
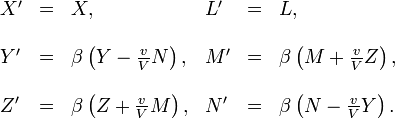
En ce qui concerne l'interpr´┐Żtation de ces ´┐Żquations, nous d´┐Żclarons ceci. Soit une masse ponctuelle d'´┐Żlectricit´┐Ż d'une grandeur unitaire dans le syst´┐Żme stationnaire K, c'est-´┐Ż-dire, dans ce syst´┐Żme stationnaire, qu'elle exerce une force de 1 dyne sur un objet similaire plac´┐Ż ´┐Ż une distance de 1´┐Żcm. En vertu du principe de relativit´┐Ż, cette masse ´┐Żlectrique mesure aussi une grandeur ´┐Ż´┐ŻunitÚá╗ dans le syst´┐Żme en mouvement. Si cette masse ´┐Żlectrique est au repos dans le syst´┐Żme stationnaire, alors la force exerc´┐Że sur elle est ´┐Żquivalente au vecteur de la force ´┐Żlectrique (X, Y, Z). Mais si cette masse ´┐Żlectrique est au repos dans le syst´┐Żme en mouvement (du moins au moment o´┐Ż elle est observ´┐Że), alors la force qui s'exerce sur elle et mesur´┐Że dans le syst´┐Żme en mouvement est ´┐Żquivalente au vecteur (X', Y', Z'). La premi´┐Żre des trois syst´┐Żmes d'´┐Żquations (1), (2) et (3) s'exprime alors comme suit´┐Ż:
1. Si une masse ponctuelle et unitaire d'´┐Żlectricit´┐Ż se d´┐Żplace dans un champ ´┐Żlectromagn´┐Żtique, alors en plus de la force ´┐Żlectrique, une ´┐Ż´┐Żforce ´┐Żlectromotrice´┐Ż´┐Ż agit sur elle, qui, en n´┐Żgligeant les termes de second ordre et sup´┐Żrieurs de v/V, est ´┐Żquivalente au produit vectoriel de la vitesse de la masse ponctuelle et de la force magn´┐Żtique divis´┐Ż par la vitesse de la lumi´┐Żre. (Ancien mode d'expression.)
2. Si une masse ponctuelle et unitaire d'´┐Żlectricit´┐Ż se d´┐Żplace dans un champ ´┐Żlectromagn´┐Żtique, alors la force qui agit sur elle est ´┐Żquivalente ´┐Ż la force ´┐Żlectrique qui existe ´┐Ż la position de la masse unitaire, que nous obtenons par la transformation du champ en un syst´┐Żme de coordonn´┐Żes qui est au repos relativement ´┐Ż la masse ´┐Żlectrique unitaire. (Nouveau mode d'expression.)
Des th´┐Żor´┐Żmes semblables faisant appel aux ´┐Ż´┐Żforces magn´┐Żtomotrices´┐Ż´┐Ż sont vrais. Dans la th´┐Żorie expos´┐Że, nous observons que la force ´┐Żlectromagn´┐Żtique joue un r´┐Żle auxiliaire, qui doit son introduction ´┐Ż la circonstance que les forces ´┐Żlectrique et magn´┐Żtique n'existent pas ind´┐Żpendamment de la nature du d´┐Żplacement dans le syst´┐Żme de coordonn´┐Żes.
De plus, il est clair que l'asym´┐Żtrie, mentionn´┐Że dans l'introduction et qui appara´┐Żt quand nous discutons du courant engendr´┐Ż par le d´┐Żplacement relatif d'un aimant et d'un conducteur, dispara´┐Żt. ´┐Żgalement, la question de l'´┐Ż´┐Żorigine´┐Ż´┐Ż des forces ´┐Żlectromotrices ´┐Żlectromagn´┐Żtiques (machine homopolaire) perd tout son sens.
´┐Ż
´┐Ż 7. Th´┐Żorie du principe de Doppler et de l'aberration

Supposons une source d'ondes ´┐Żlectromagn´┐ŻtiquesNdT 6 dans le syst´┐Żme K ´┐Ż une grande distance de l'origine, mod´┐Żlis´┐Że avec une bonne approximation dans une partie de l'espace qui contient l'origine par les ´┐Żquations´┐Ż:
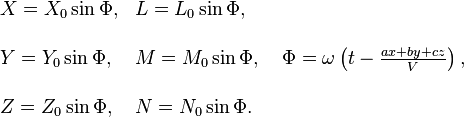
Ici (X0, Y0, Z0) et (L0, M0, N0) sont les vecteurs qui d´┐Żterminent l'amplitude du train d'ondes et (a, b, c) sont les cosinus directeurs des normales ´┐Ż l'onde.
Questionnons-nous sur la composition de ces ondes, quand elles sont observ´┐Żes par un observateur au repos dans le syst´┐Żme en mouvement k. En appliquant les ´┐Żquations de transformation obtenues au ´┐Ż 6 pour les forces ´┐Żlectrique et magn´┐Żtique, et les ´┐Żquations de transformation obtenues au ´┐Ż 3 pour les coordonn´┐Żes et le temps, il vient imm´┐Żdiatement´┐Ż:
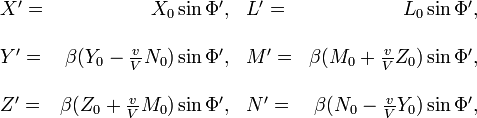
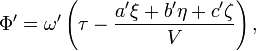
o´┐Ż
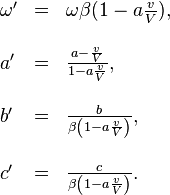
De l'´┐Żquation donnant ω' , il r´┐Żsulte que si un observateur se d´┐Żplace ´┐Ż une vitesse v relativement ´┐Ż une source lumineuse situ´┐Że ´┐Ż une distance infinie qui ´┐Żmet des ondes d'une fr´┐Żquenceν, de telle fa´┐Żon que la ligne qui joint la source de la lumi´┐Żre et l'observateur fait un angle φ avec la vitesse de l'observateur rapport´┐Że ´┐Ż un syst´┐Żme de coordonn´┐Żes qui est stationnaire en regard de la source, alors la fr´┐Żquence ν' per´┐Żue par l'observateur se calcule par la formule´┐Ż:
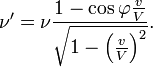
C'est le principe de Doppler pour toute vitesse.
Si φ = 0, alors l'´┐Żquation prend une forme plus simple´┐Ż:
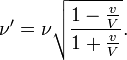
Nous observons que ´┐Ż´┐Żcontrairement ´┐Ż la conception courante´┐Ż´┐Ż si v = -V, alors ν' = ∞NdT 7.
Si φ' est l'angle entre la normale de l'onde (direction du rayon) dans le syst´┐Żme en mouvement et le segment ´┐Ż´┐Żsource-observateur lumi´┐Żre´┐Ż´┐Ż, l'´┐Żquation pour a' prend la forme
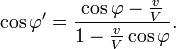
Cette ´┐Żquation exprime la loi de l'aberration sous sa forme la plus g´┐Żn´┐Żrale. Si φ = π/2, alors elle prend la forme simple´┐Ż:
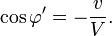
Nous devons toujours trouver l'amplitude des ondes qui apparaissent dans le syst´┐Żme en mouvement. Si A et A' sont les forces (´┐Żlectrique et magn´┐Żtique) mesur´┐Żes dans les syst´┐Żmes stationnaire et en mouvement, nous avons
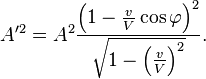
Si φ = 0, alors elle se r´┐Żduit ´┐Ż la forme simple
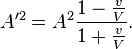
En s'appuyant sur ces ´┐Żquations, il semble que pour un observateur, qui se d´┐Żplace ´┐Ż la vitesse V vers la source de lumi´┐Żre, cette source lui appara´┐Żtra infiniment intense.
´┐Ż
´┐Ż 8. Transformation de l'´┐Żnergie des rayons lumineux. Th´┐Żorie de la pression de radiation exerc´┐Że sur un miroir parfait

Puisque A2/8π est ´┐Żgal ´┐Ż l'´┐Żnergie de la lumi´┐Żre par unit´┐Ż de volume, nous devons (selon le principe de relativit´┐Ż) consid´┐Żrer A'2/8π comme l'´┐Żnergie de la lumi´┐Żre dans le syst´┐Żme en mouvement. En cons´┐Żquence, A'2/A2 d´┐Żfinit le rapport entre les ´┐Żnergies d'un complexe de lumi´┐ŻreNdT 8 born´┐Ż ´┐Ż´┐Żmesur´┐Ż lorsqu'en mouvement´┐Ż´┐Ż et ´┐Ż´┐Żmesur´┐Ż lorsque stationnaire´┐Ż´┐Ż, les volumes du complexe de lumi´┐Żre mesur´┐Żs dans K et k ´┐Żtant ´┐Żgaux. Or, ce n'est pas le cas. Si a, b, c sont les cosinus directeurs des normales ´┐Ż l'onde lumineuse dans le syst´┐Żme stationnaire, alors aucune ´┐Żnergie ne traverse les ´┐Żl´┐Żments de la surface sph´┐Żrique
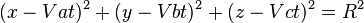
qui se d´┐Żplace ´┐Ż la vitesse de la lumi´┐Żre. Nous pouvons donc affirmer que cette surface contient toujours le m´┐Żme complexe de lumi´┐Żre. Analysons la quantit´┐Ż d'´┐Żnergie que cette surface renferme, quand elle est observ´┐Że du syst´┐Żme k, c'est-´┐Ż-dire l'´┐Żnergie du complexe de lumi´┐Żre relativement au syst´┐Żme k.
Observ´┐Że depuis le syst´┐Żme en mouvement, la surface sph´┐Żrique devient ellipso´┐Żdale et respecte, au temps τ = 0, l'´┐Żquation´┐Ż:
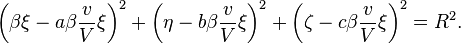
Si S d´┐Żsigne le volume de la sph´┐Żre et S' le volume de cet ellipso´┐Żde, alors un simple calcul montre que
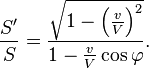
Si E repr´┐Żsente l'´┐Żnergie lumineuse mesur´┐Że dans le syst´┐Żme stationnaire et E' l'´┐Żnergie mesur´┐Że dans le syst´┐Żme en mouvement, born´┐Żes par les surfaces d´┐Żcrites plus haut, alors
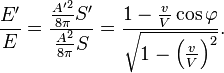
Si φ = 0, nous obtenons une formule plus simple´┐Ż:
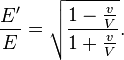
Remarquons que l'´┐Żnergie et la fr´┐Żquence du complexe de lumi´┐Żre varient selon la m´┐Żme loi que l'´┐Żtat de mouvement de l'observateur.
Soit un parfait miroir r´┐Żfl´┐Żchissant dans le plan de coordonn´┐Żes ξ=0, ´┐Ż partir duquel l'onde plane ´┐Żtudi´┐Że dans le paragraphe pr´┐Żc´┐Żdent est r´┐Żfl´┐Żchie. Demandons-nous quelle pression de radiation s'exerce sur la surface r´┐Żfl´┐Żchissante, ainsi que la direction, la fr´┐Żquence et l'intensit´┐Ż de la lumi´┐Żre apr´┐Żs la r´┐Żflexion.
Soit la lumi´┐Żre incidente d´┐Żfinie par les grandeurs A, cos φ, ν (dans le syst´┐Żme K). Observ´┐Żes de k, nous avons les grandeurs correspondantes´┐Ż:
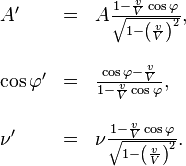
Pour la lumi´┐Żre r´┐Żfl´┐Żchie, nous obtenons, quand le ph´┐Żnom´┐Żne est observ´┐Ż du syst´┐Żme k´┐Ż:
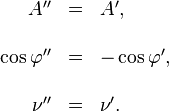
En appliquant une transformation inverse au syst´┐Żme stationnaire K, nous obtiendrons pour la lumi´┐Żre r´┐Żfl´┐Żchie´┐Ż:

L'´┐Żnergie qui tombe sur une unit´┐Ż de surface du miroir par unit´┐Ż de temps (mesur´┐Że dans le syst´┐Żme stationnaire) est ´┐Żvidemment (A2 / 8 π) (V cos φ - v). La quantit´┐Ż d'´┐Żnergie qui en rayonne par unit´┐Ż de surface du miroir par unit´┐Ż de temps est (A''' 2 / 8 π) (-V cos φ''' + v). La diff´┐Żrence entre ces deux expressions est, selon le principe de l'´┐Żnergie, la quantit´┐Ż de travail accomplie par la pression de radiation par unit´┐Ż de temps. Si nous la posons ´┐Żgale ´┐Ż P.v, o´┐Ż P est la pression de radiation, nous avons
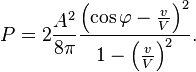
Par l'approximation au premier ordre, nous obtenons
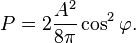
qui est en accord avec les observations et d'autres th´┐Żories.
Tous les probl´┐Żmes d'optique des corps en mouvement peuvent ´┐Żtre r´┐Żsolus en appliquant les m´┐Żthodes expos´┐Żes ici. Le point crucial est que toutes les forces ´┐Żlectriques et magn´┐Żtiques de la lumi´┐Żre, qui sont influenc´┐Żes par un corps en mouvement, devraient ´┐Żtre transform´┐Żes dans un syst´┐Żme de coordonn´┐Żes stationnaire relativement au corps. De cette fa´┐Żon, tous les probl´┐Żmes optiques de corps en mouvement seraient r´┐Żduits ´┐Ż une suite de probl´┐Żmes d'optique de corps au repos.
´┐Ż
´┐Ż 9. Transformations des ´┐Żquations de Maxwell-Hertz
en ce qui concerne les courants de convection

Commen´┐Żons par ces ´┐Żquations´┐Ż:
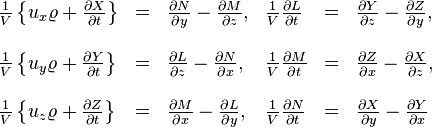
o´┐Ż
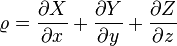
indique 4π fois la densit´┐Ż de l'´┐Żlectricit´┐Ż et (ux, uy, uz) est le vecteur vitesse de l'´┐Żlectricit´┐Ż. Si nous supposons que les masses ´┐Żlectriques sont li´┐Żes de fa´┐Żon permanente ´┐Ż de petits corps rigides (ions ou ´┐Żlectrons, par exemple), alors ces ´┐Żquations forment le fondement ´┐Żlectromagn´┐Żtique de l'´┐Żlectrodynamique et de l'optique des corps en mouvement de Lorentz.
Si ces ´┐Żquations, vraies dans le syst´┐Żme K, sont transform´┐Żes pour le syst´┐Żme k ´┐Ż l'aide des ´┐Żquations de transformations donn´┐Żes aux ´┐Ż 3 et ´┐Ż 6, alors nous obtenons les ´┐Żquations´┐Ż:
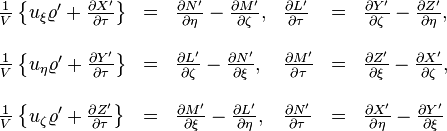
o´┐Ż
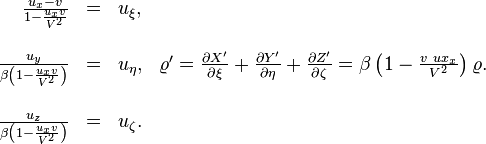
Puisque le vecteur (uξ, uη, uζ) n'est rien d'autre que la vitesse de la masse ´┐Żlectrique mesur´┐Że dans le syst´┐Żme k, qui est une cons´┐Żquence du th´┐Żor´┐Żme d'addition des vitesses du ´┐Ż 5, alors il est d´┐Żmontr´┐Ż que, en prenant notre principe cin´┐Żmatique comme base, le fondement ´┐Żlectromagn´┐Żtique de la th´┐Żorie de Lorentz de l'´┐Żlectrodynamique des corps en mouvement correspond au principe de relativit´┐Ż.
Nous pouvons bri´┐Żvement remarquer qu'une loi importante d´┐Żcoule ais´┐Żment des ´┐Żquations d´┐Żvelopp´┐Żes´┐Ż: si un corps ´┐Żlectriquement charg´┐Ż se d´┐Żplace de quelque fa´┐Żon que ce soit dans l'espace et si sa charge est invariable, quand observ´┐Że depuis un syst´┐Żme qui se d´┐Żplace de la m´┐Żme fa´┐Żon, alors la charge demeure constante m´┐Żme si elle observ´┐Że depuis le syst´┐Żme stationnaire K.
´┐Ż
´┐Ż 10. Dynamique de l'´┐Żlectron (lentement acc´┐Żl´┐Żr´┐Ż)

Supposons qu'une particule ponctuelle qui poss´┐Żde la charge ´┐Żlectrique ε (que nous appellerons dor´┐Żnavant ´┐Ż´┐Ż´┐Żlectron´┐Ż´┐Ż) se d´┐Żplace dans un champ ´┐Żlectromagn´┐Żtique. Nous faisons l'hypoth´┐Żse suivante pour sa loi de d´┐Żplacement.
Si l'´┐Żlectron est au repos ´┐Ż une p´┐Żriode de temps bien d´┐Żfinie, alors pendant la prochaine parcelle de temps, le mouvement respecte les ´┐Żquations
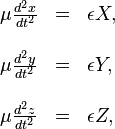
o´┐Ż x, y, z sont les coordonn´┐Żes de l'´┐Żlectron et μ sa masse, du moment qu'il se d´┐Żplace lentement.
Supposons que l'´┐Żlectron se d´┐Żplace ´┐Ż une vitesse v ´┐Ż une certaine p´┐Żriode de temps. Analysons les lois selon lesquelles l'´┐Żlectron se d´┐Żplacera pendant la parcelle de temps qui suit imm´┐Żdiatement.
Sans modifier la port´┐Że g´┐Żn´┐Żrale de notre discussion, nous pouvons et ferons l'hypoth´┐Żse que, au moment que nous analysons, l'´┐Żlectron est ´┐Ż l'origine du syst´┐Żme de coordonn´┐Żes, puis se d´┐Żplace ´┐Ż la vitesse v selon l'axe des x du syst´┐Żme K. Il est ´┐Żvident qu'´┐Ż ce moment (t=0), l'´┐Żlectron est au repos relativement au syst´┐Żme k, qui se d´┐Żplace parall´┐Żlement ´┐Ż l'axe des x ´┐Ż la vitesse constante v.
´┐Ż partir des hypoth´┐Żses faites plus haut, en association avec le principe de relativit´┐Ż, il est ´┐Żvident qu'observ´┐Ż depuis le syst´┐Żme k, l'´┐Żlectron ´┐Ż´┐Żpendant la parcelle de temps imm´┐Żdiatement cons´┐Żcutive (pour une petite valeur de t)´┐Ż´┐Ż se d´┐Żplace selon les ´┐Żquations
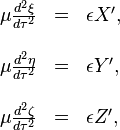
o´┐Ż les symboles ξ, η, ζ, τ, X', Y', Z' se rapportent au syst´┐Żme k. Si nous fixons t = x = y = z = 0 et τ = ξ = η = ζ = 0, alors les ´┐Żquations de transformation donn´┐Żes aux ´┐Ż´┐Ż 3 et 6 sont vraies. Nous avons´┐Ż:
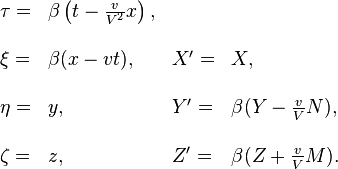
´┐Ż l'aide de ces ´┐Żquations, nous pouvons transformer les ´┐Żquations du mouvement plus haut du syst´┐Żme k au syst´┐Żme K et obtenir´┐Ż:
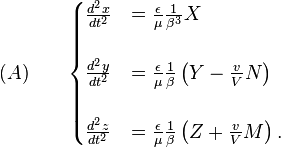
Questionnons-nous, suivant la m´┐Żthode habituelle de calculs, sur les masses longitudinale et transversale d'un ´┐Żlectron en mouvement. Nous r´┐Ż´┐Żcrivons les ´┐Żquations (A) sous la forme
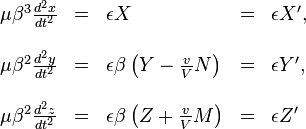
et observons tout de suite que εX', εY', εZ' sont les composantes de la force pond´┐Żromotrice qui agit sur l'´┐Żlectron et sont consid´┐Żr´┐Żes dans un syst´┐Żme en mouvement qui, ´┐Ż ce moment, se d´┐Żplace ´┐Ż la m´┐Żme vitesse que l'´┐Żlectron. (Cette force peut, par exemple, ´┐Żtre mesur´┐Że par une balance ´┐Ż ressort au repos dans ce syst´┐Żme.) Si nous appelons bri´┐Żvement cette force la ´┐Ż´┐Żforce qui agit sur l'´┐Żlectron´┐Ż´┐Ż, et continuons avec cette ´┐Żquation´┐Ż:
Valeur de la masse ´┐Ż valeur de l'acc´┐Żl´┐Żration = Valeur de la force,
et si nous d´┐Żfinissons de plus que les acc´┐Żl´┐Żrations sont mesur´┐Żes dans le syst´┐Żme stationnaire K, alors ´┐Ż partir des ´┐Żquations plus haut, nous obtenons´┐Ż:
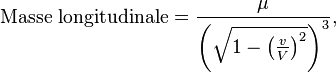
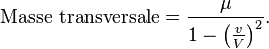
Naturellement, quand la force et l'acc´┐Żl´┐Żration sont d´┐Żfinies autrement, d'autres valeurs sont obtenues pour la masse. Donc, nous voyons que nous devons proc´┐Żder avec beaucoup de pr´┐Żcautions lorsque nous comparons diff´┐Żrentes th´┐Żories du mouvement de l'´┐Żlectron.
Observons que ce r´┐Żsultat sur la masse est ´┐Żgalement vrai pour une masse de mati´┐Żre pond´┐Żrable´┐Ż; parce qu'un point mat´┐Żriel pond´┐Żrable peut ´┐Żtre converti en ´┐Żlectron (pour nos sens) en lui ajoutant une charge ´┐Żlectrique aussi petite que l'on veut.
D´┐Żterminons maintenant l'´┐Żnergie cin´┐Żtique d'un ´┐Żlectron. Si l'´┐Żlectron se d´┐Żplace ´┐Ż partir de l'origine des coordonn´┐Żes d'un syst´┐Żme K ´┐Ż la vitesse initiale de 0 de fa´┐Żon r´┐Żguli´┐Żre selon l'axe des x sous l'action d'une force ´┐Żlectrostatique X, alors il est ´┐Żvident que l'´┐Żnergie tir´┐Że du champ ´┐Żlectrostatique est la valeur ∫ εX dx. Puisque l'´┐Żlectron devrait ´┐Żtre acc´┐Żl´┐Żr´┐Ż lentement et donc qu'aucune ´┐Żnergie n'est perdue sous la forme de radiation, alors l'´┐Żnergie tir´┐Że du champ ´┐Żlectrostatique doit ´┐Żgaler l'´┐Żnergie W du d´┐Żplacement. Consid´┐Żrant l'ensemble du ph´┐Żnom´┐Żne de mouvement ´┐Ż l'´┐Żtude, la premi´┐Żre des ´┐Żquations de (A) est vraie. Nous avons´┐Ż:
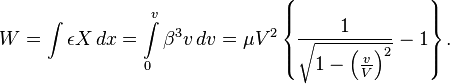
Lorsque v=V, W est infiniment grand. Comme nos r´┐Żsultats ant´┐Żrieurs le montrent, toute vitesse supraluminique est impossible.
En tant que cons´┐Żquence des arguments ´┐Żcrits plus haut, cette expression pour l'´┐Żnergie cin´┐Żtique doit aussi ´┐Żtre vraie pour les masses pond´┐Żrables.
Nous sommes ´┐Ż m´┐Żme d'´┐Żnum´┐Żrer les caract´┐Żristiques du mouvement des ´┐Żlectrons qui peuvent ´┐Żtre v´┐Żrifi´┐Żes exp´┐Żrimentalement, lesquelles d´┐Żcoulent du syst´┐Żme d'´┐Żquations (A).
1. De la deuxi´┐Żme ´┐Żquation en (A), il d´┐Żcoule qu'une force ´┐Żlectrique Y et une force magn´┐Żtique N produisent la m´┐Żme d´┐Żflexion d'un ´┐Żlectron se d´┐Żpla´┐Żant ´┐Ż la vitesse v quand Y = N.v/V. En cons´┐Żquence, nous voyons qu'il est possible de mesurer la vitesse d'un ´┐Żlectron en calculant le rapport de la d´┐Żflexion magn´┐Żtique Am et de la d´┐Żflexion ´┐Żlectrique Ae, en accord avec notre th´┐Żorie pour toute vitesse arbitraire, en appliquant la loi´┐Ż:
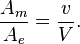
Cette relation peut ´┐Żtre test´┐Że exp´┐Żrimentalement car la vitesse de l'´┐Żlectron peut ´┐Żtre directement mesur´┐Że ´┐Ż l'aide, par exemple, de champs ´┐Żlectriques et magn´┐Żtiques oscillant rapidement.
2. ´┐Ż partir de la valeur de l'´┐Żnergie cin´┐Żtique de l'´┐Żlectron, il suit que si ce dernier subit une diff´┐Żrence de potentiel P, cette derni´┐Żre est li´┐Że ´┐Ż la vitesse v par la relation suivante´┐Ż:
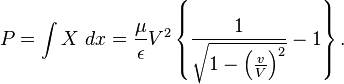
3. Nous calculons le rayon de courbure R du chemin, o´┐Ż la force magn´┐Żtique N est la seule force de d´┐Żflexion qui agit perpendiculairement ´┐Ż la vitesse de projection. De la seconde ´┐Żquation en (A), nous obtenons´┐Ż:
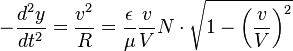
ou
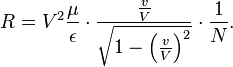
Ces trois relations expriment compl´┐Żtement la loi du mouvement de l'´┐Żlectron selon la th´┐Żorie expos´┐Że plus haut.
En terminant, je tiens ´┐Ż souligner que mon ami et coll´┐Żgue M. Besso m'a pr´┐Żt´┐Ż son concours pendant que je travaillais au probl´┐Żme discut´┐Ż ici, et que je lui suis redevable de suggestions pr´┐Żcieuses.
Berne, juin 1905
(Re´┐Żu le 30 juin 1905.)
´┐Ż
Notes

- L'inexactitude, inh´┐Żrente au concept de simultan´┐Żit´┐Ż de deux ´┐Żv´┐Żnements (presque) au m´┐Żme endroit, et qui doit ´┐Żgalement ´┐Żtre r´┐Żsolue par une abstraction, n'est pas discut´┐Że ici.
- Ici, le terme ´┐Ż´┐Żtemps´┐Ż´┐Ż indique indiff´┐Żremment ´┐Ż´┐Żtemps dans le syst´┐Żme stationnaire´┐Ż´┐Ż et ´┐Ż´┐Żposition des aiguilles d'une horloge en mouvement´┐Ż´┐Ż situ´┐Że ´┐Ż la position en question.
- C'est-´┐Ż-dire qui poss´┐Żde une forme sph´┐Żrique lorsque observ´┐Że dans le syst´┐Żme stationnaire.
- Si par exemple X = Y = Z = L = M = 0 et N ≠ 0, alors pour des raisons de sym´┐Żtrie il est clair que, en changeant le signe de v sans modifier sa valeur absolue, Y' doit aussi changer de signe sans changer de valeur absolue.
Notes du traducteur

- En jargon moderne, il s'agit de l'´┐Żther luminif´┐Żre.
- Par ´┐Ż espace vide ´┐Ż, il faut comprendre ´┐Ż vide parfait ´┐Ż, que l'on peut presque assimiler ´┐Ż l'espace intersid´┐Żral d´┐Żnu´┐Ż de toute mati´┐Żre.
- En anglais, il est ´┐Żcrit ´┐Ż measuring rod ´┐Ż, qui se traduit litt´┐Żralement par ´┐Ż tige ´┐Ż mesurer ´┐Ż. Le terme ´┐Ż r´┐Żgle ´┐Ż mesurer ´┐Ż est plus pr´┐Żs du sens recherch´┐Ż.
- Dans sa traduction, Maurice Solovine pr´┐Żf´┐Żre ´┐Ż mouvement de translation uniforme ´┐Ż, selon le nom de l'une des transformations g´┐Żom´┐Żtriques. La terminologie physique pr´┐Żf´┐Żre ´┐Ż mouvement rectiligne uniforme ´┐Ż.
- En jargon moderne, il s'agit d'un syst´┐Żme de coordonn´┐Żes cart´┐Żsiennes en 3´┐Żdimensions.
- Dans le texte en anglais, il est ´┐Żcrit ´┐Ż electrodynamic ´┐Ż, mais dans l'article, il est seulement fait mention des th´┐Żories de Maxwell, Hertz ou Lorentz, qui traitent toutes d'ondes ´┐Żlectromagn´┐Żtiques.
- L'´┐Żquation est corrig´┐Że selon ce qui est ´┐Żcrit dans la traduction de Maurice Solovine.
- Selon Yves Pierseaux dans La "Structure fine" de la Relativit´┐Ż Restreinte (Harmattan, 1er juillet 1999, p.´┐Ż300), Einstein introduit le terme ´┐Ż complexe de lumi´┐Żre ´┐Ż ´┐Ż ce moment-ci de l'article, puis, apr´┐Żs la publication de cet article, il pr´┐Żf´┐Żre ´┐Ż syst´┐Żme d'ondes planes ´┐Ż. Le jargon moderne pr´┐Żf´┐Żre ´┐Ż´┐Żpaquet d'onde´┐Ż´┐Ż.
Ouvrages

- (de) A. Einstein, ´┐Ż´┐ŻZur Elektrodynamik bewegter K´┐Żrper´┐Ż´┐Ż, dans Annalen der Physik, vol.´┐Ż322, no´┐Ż10, 26´┐Żseptembre´┐Ż1905, p.´┐Ż891-921 (ISSN 0003-3804) texte int´┐Żgral, lien DOI (fichier au format PDF)
- (en) Contributeurs, ´┐Ż´┐ŻOn the Electrodynamics of Moving Bodies (1920 edition)´┐Ż´┐Ż, Wikisource, 2012.
- (en) Contributeurs, ´┐Ż´┐ŻOn the Electrodynamics of Moving Bodies´┐Ż´┐Ż, 14´┐Żavril´┐Ż2011.
- Albert Einstein (trad. Maurice Solovine), ´┐Ż Sur l'´┐Żlectrodynamique des corps en mouvement ´┐Ż, dans Einstein : Sur l'´┐Żlectrodynamique des corps en mouvement + 6 textes sur la Th´┐Żorie de la Relativit´┐Ż, ´┐Żditions Jacques Gabay, 1994, 160´┐Żp. (ISBN 978-2-87647-155-9).












![\frac{1}{2}\left[\tau(0,0,0,t)+\tau\left(0,0,0,\left\{ t+\frac{x'}{V-v}+\frac{x'}{V+v}\right\} \right)\right]](Electrodynamique_files/image007.gif)