Rachad ANTONIUS, Considérations pédagogiques sur l’enseignement des statistiques en sciences humaines

Rachad ANTONIUS

sociologue, professeur, Département de sociologie, UQÀM.

“Considérations pédagogiques
sur l’enseignement
des statistiques en sciences humaines”.

(Notes de présentation provisoires)

Montréal, Notes dans le cadre d’un séminaire CDAME [Collectif pour le développement et les applications en mesure et évaluation], UQAM, 21 février 2013, 12 pp.

Introduction

Fondements pédagogiques de la méthode

Les différences entre moyennes : quand sont-elles statistiquement significatives ?

L’interprétation des résultat d’une ANOVA à deux facteurs

Effet principal simple

Illustration de la dimension d'un ensemble de données dans une analyse factorielle

Conclusion

INTRODUCTION

Les questions qui guident la présente réflexion sont les suivantes :

Comment mettre à profit l’intuition – de façon efficace – dans la transmission de notions de statistiques plutôt complexes ? Comment utiliser les représentations visuelles pour développer l’intuition ?

L’approche présentée ici résulte d’une longue expérience d’enseignement des mathématiques au niveau collégial. Une leçon majeure que je tire de cette expérience est à l’effet qu’une des choses les plus difficiles, dans l’enseignement des mathématiques ou des statistiques, c’est de réaliser que ce qui va de soi pour quelqu’un de familier avec la matière, n’est pas du tout évident pour les débutants. Le bon sens en mathématiques n’est pas inné : il doit être développé patiemment. J’ai donc développé une méthode ad hoc, fondée d’abord sur l’introspection concernant mes propres difficultés lorsque je faisais des mathématiques avancées (3^e cycle) et sur la réflexion et l’expérimentation lors de mon enseignement des mathématiques au collégial. C’est cet apprentissage que j’ai transposé dans le domaine des statistiques appliquées aux sciences humaines, que je préfère désigner par le terme méthodes quantitatives, pour bien souligner la réflexion méthodologique qui sous-tend la démarche. La méthode se distingue de la technique en ce qu’elle inclut une réflexion sur les conditions d’application de la technique, et sur ses limites de validité. Par ailleurs, il faut constamment expliquer aux étudiants que ce n’est pas l’usage de données quantitatives et de statistiques, aussi sophistiquées soient-elles, qui confère un caractère scientifique à un texte, mais bien le cadre conceptuel et théorique à partir duquel les mesures sont conçues et interprétées. En d’autres termes, c’est l’aspect qualitatif et conceptuel d’une recherche qui donne sens aux chiffres, et pas le contraire. On pourrait dire que c’est une posture non-positiviste que j’adopte quand j’aborde les statistiques.

FONDEMENTS PÉDAGOGIQUES
DE LA MÉTHODE

La méthode développée ici – de façon ad hoc, rappelons-le ; je ne suis pas spécialiste de la didactique ou de la pédagogie – est fondée sur les idées suivantes.

1. La connaissance se construit par des processus inductifs et des processus déductifs, qui ont des rôles différents dans l’apprentissage. Les processus inductifs sont plus efficaces quand le sujet est nouveau, que la pertinence des questions auxquelles on répond n’a pas encore été établie, ou que la maturité nécessaire à l’apprentissage par une organisation déductive de la matière à apprendre n’a pas été atteinte. L’induction correspond à l’étape de la découverte, du changement de paradigme, de la compréhension d’un sujet nouveau. La déduction convient à l’étape de la mise en ordre des concepts, des idées et des théories, à l’organisation efficace (i.e. économe) du savoir, ainsi qu’à la preuve.

Pour l’enseignement des méthodes quantitatives à un public non spécialisé, nous postulons que c’est l’induction qui est primordiale.

2. La démonstration de la pertinence d’une question doit précéder l’articulation d’une réponse à cette question. Ceci est une autre façon de dire qu’une réponse n’a de sens que si la question a été intériorisée. Démontrer la pertinence d’une question, c’est avant tout montrer sa signification, c’est-à-dire :

a) son sens,
b) son importance par rapport à d’autres questions, et

c) les conséquences que pourraient avoir les réponses possibles par rapport au sujet traité.

3. L’importance des schémas et de la représentation visuelle, qui replacent les concepts dans une structure significative qui les relie entre eux. Ceci est particulièrement vrai des concepts systémiques (par opposition aux concepts empiriques, distinction admirablement expliquée dans un ouvrage passé de mode : The Conduct of Inquiry d’Abraham Kaplan) qui ne prennent leur sens que par rapport à d’autres concepts et qui ne peuvent être définis de façon isolée. Mais c’est aussi vrai de questions plus simples, tel que le lien entre l’échelle de mesure de deux variables et la méthode utilisée pour mesurer l’association statistique entre elles.

4. La traduction des résultats numériques en mots, en phrases complètes qui expriment et explicitent le sens des nombres obtenus, et une étape fondamentale de l’apprentissage. Nous avons trop souvent tendance à prendre pour acquis que la correspondance entre les nombres et les objets qu’ils représentent est claire pour nos étudiants, mais souvent, ce n’est pas le cas. (Ce principe est mis en application avec la lecture des tableaux croisés, par exemple).

5. Nous constatons que l’ordre de présentation des sujets dans la plupart des manuels de statistiques suit une logique déductive, axée sur la preuve, ce qui est absolument nécessaire pour la formation de statisticiens. Mais pour la formation d’usagers des méthodes statistiques en sciences humaines (et sans doute dans d’autres domaines aussi), il faut un autre ordre de présentation, qui établit en premier le sens des affirmations à démontrer, ensuite leur pertinence, et en dernier lieu, si le temps le permet, la preuve de leur exactitude. La qualité scientifique des méthodes enseignées ainsi est garantie par des preuves mathématiques, mais il n’est pas nécessaire d’inclure ces preuves pour un cours destiné aux usagers. La relaxation de cette exigence permet un renversement de la succession des étapes et des sujets enseignés, de façon à satisfaire une logique fondée sur la communication, en priorité, du sens des résultats obtenus, par opposition à la communication de la preuve en premier lieu. Les procédures d’estimation fournissent un exemple parfait de cette situation : on peut très bien comprendre la logique de l’estimation, et le rapport entre le degré de précision de l’estimé et le niveau de risque que l’on prend en le faisant, avant de savoir calculer l’un ou l’autre.

6. En particulier l’ordre de succession des étapes d’une recherche n’est pas l’ordre de la compréhension de ces étapes. Certaines détails techniques (tel que la façon de définir une variable dans SPSS) ne deviennent intelligibles que lorsqu’on a eu à faire des analyses et qu’on a compris la pertinence de faire des distinctions entre les variables en fonction de leur niveau de mesure. Si on suit une logique déductive et linéaire, il faudrait apprendre à définir des variables dans SPSS, et ensuite seulement apprendre à analyser les données numériques correspondant à ces variables. Nous pensons au contraire qu’il faut apprendre à décrire des données numériques d’abord, et que c’est cela qui permettra de comprendre pourquoi il faut déterminer l’échelle de mesure d’une variable dès sa définition dans SPSS, avant de saisir les données. Effectivement, notre laboratoire sur la saisie des données ne vient que bien après les laboratoires où on met en pratique des analyses descriptives.

7. Nous pensons qu’une démarche qui va de l’intuition à la formalisation, et non le contraire, est plus efficace avec des étudiants qui n’ont pas atteint une certaine maturité intellectuelle et une maîtrise minimale de l’arithmétique. On commence donc par exploiter au maximum des notions intuitives, on identifie leurs faiblesses, leurs incohérences ou leurs limites, et on propose ensuite des notions rigoureuses comme réponse à ces faiblesses. La formalisation (et la preuve) apparaissent alors comme une réponse aux limites de l’intuition. Cette stratégie est utilisée de façon systématique. Elle peut être justifiée par le recours à la notion de maturité expliquée au point suivant. Le cheminement de l’intuition vers la formalisation est un processus de maturation intellectuelle.

8. La maturité : c’est la capacité de combler des lacunes épistémologiques, dans le sens suivant. Ceux et celles qui ont étudié des mathématiques un tant soit peu avancées savent qu’une démonstration qui part des axiomes d’une théorie et qui établit des conclusions de façon déductive peut être mathématiquement parfaite, mais incompréhensible pour un non-mathématicien. Pourtant, elle ne fait appel à aucune connaissance formelle autre que celles qu’elle postule comme axiomes de départ. Théoriquement, elle serait compréhensible par tout le monde. Ce qui manque aux non-mathématiciens, c’est la maturité, c’est-à-dire la capacité de percevoir le sens et la pertinence de la démonstration. Or la maturité s’acquiert par l’expérience, et elle est fondée sur l’analogie entre la situation étudiée et d’autres situations similaires ou ressemblantes. Elle suppose donc une intégration des connaissances, c’est-à-dire une compréhension de leur signification suivie d’une rétention puis d’un transfert. La maturité s’acquiert par une exposition à de nombreux cas présentant des analogies, d’où on peut tirer des leçons communes mais qui ne sont pas nécessairement explicites. Ces leçons interviennent dans la compréhension d’une démonstration nouvelle ; c’est cela la maturité. La maturité est donc spécifique à un champ de connaissance donné.

Notons que ces principes pédagogiques sont mis en pratique par de nombreux enseignants, de manière plus ou moins consciente, plus ou moins systématique, et plus ou moins explicite. Nous n’avons rien inventé. Mais ayant identifié ces stratégies pédagogiques, nous avons essayé de les mettre en forme et de les appliquer systématiquement.

Ceci est fait en particulier dans l’ouvrage suivant : Antonius, R. (2013) Interpreting Quantitative Data with IBM SPSS Statistics, London, SAGE Publications, 343 p.

Dans ce qui suit, nous avons illustré la méthode préconisée par quelques exemples.

LES DIFFÉRENCES ENTRE MOYENNES :
QUAND SONT-ELLES STATISTIQUEMENT
SIGNIFICATIVES ?

Idée à communiquer aux étudiants : Pourquoi il faut prendre en ligne de compte la dispersion des données pour déterminer si une différence de moyennes est statistiquement significative.

Pour illustrer cette idée et la communiquer, il faut auparavant que les étudiants aient une bonne idée de la notion de distribution d’échantillonnage. Il faut qu’ils sachent que si on prend tous les échantillons possibles et imaginables de taille n tirés d’une même population, et que l’on mesure une statistique quelconque sur chacun des échantillons (par exemple la moyenne, ou une proportion), les diverses valeurs prises par cette statistique sur l’ensemble des échantillons forment une distribution qu’on appelle la distribution d’échantillonnage. On connaît la forme de cette distribution ainsi que ses propriétés pour un certain nombre de statistiques. Les valeurs prises par la statistique sur les divers échantillons se répartissent donc tout au long de l’étendue de cette distribution. On peut connaître la probabilité avec laquelle cette statistique tombera dans un intervalle donné dans la distribution. On dira par abus de langage que l’échantillon tombe dans cet intervalle, pour signifier que la statistique calculée sur l’échantillon tombe dans cet intervalle. Cette situation peut être illustrée par le diagramme suivant, qui résume la conclusion principale d’une présentation sur la distribution d’échantillonnage, présentation qui se fera elle aussi à l’aide de nombreux diagrammes et représentations visuelles. Mais ce n’est pas l’objet de la présente discussion. Donc on se contentera de montrer le résultat de cette discussion, donné par les deux diagrammes suivants.

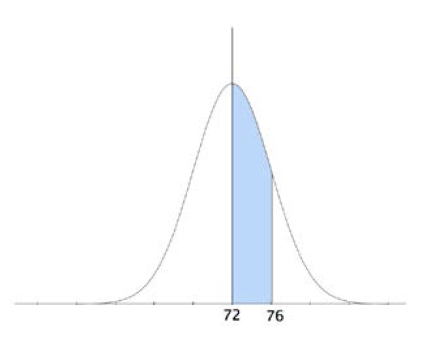
$C:\Users\Rachad\Dropbox\Projet SAGE 2011\Manuscript May 2011\Diagrams normal curve\Normal curve with shade 72 76.jpg$

Lorsqu’une distribution d’échantillonnage est connue, on peut déterminer avec précision le pourcentage d’échantillons pour lesquels la statistique mesurée tombe dans la partie colorée en bleu, pour n’importe quelles valeurs de x (ici se sont les valeurs 72 et 76, dans une distribution centrée autour de 72 et ayant un écart type de 4 unités). Ceci signifie que la probabilité qu’un échantillon tiré au hasard tombe dans la région colorée peut être calculée avec précision, et c’est la surface de la partie colorée divisée par la surface totale sous la courbe.

Dans cette distribution d’échantillonnage, 2.5% des échantillons tombent au-delà de la valeur 1.96, de part ou d’autre de la courbe.

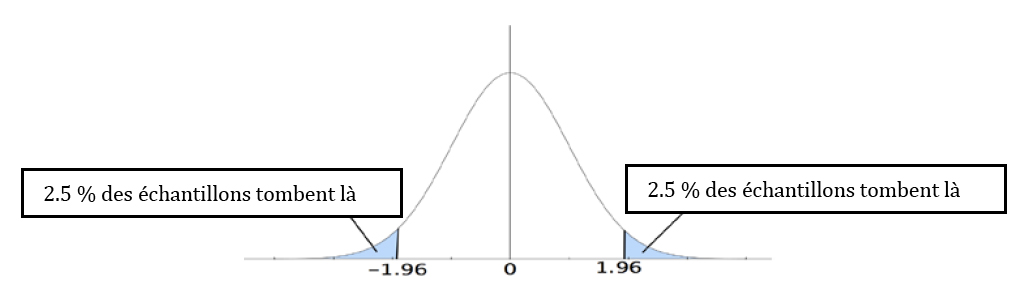
En particulier, quand on connaît les propriétés d’une distribution d’échantillonnage, on peut savoir la valeur spécifique à partir de laquelle les 5% des échantillons les plus extrêmes se retrouvent. Dans la figure qui précède, ces 5% sont répartis également à gauche et à droite de la courbe. L’inférence statistique est fondée sur la compréhension de cet énoncé.

Abordons maintenant la question qui nous intéresse, celle d’illustrer pourquoi les variances des valeurs observées dans deux échantillons doivent être prises en ligne de compte pour décider si une différence de moyennes est statistiquement significative. L’hypothèse nulle est à l’effet que les deux échantillons proviennent d’une même population. Or leurs moyennes diffèrent. Est-ce que cette différence contredit l’hypothèse (nulle), qui énonce qu’ils proviennent de la même population ? Il se pourrait bien que la différence observée entre les deux moyennes soit simplement le résultat du hasard : aucun des deux échantillons n’est une réplique exacte de la population, donc on peut s’attendre à ce qu’ils diffèrent un peu de la population et donc qu’ils diffèrent un peu entre eux. Mais c’est combien, un peu ? S’ils diffèrent beaucoup on dira : attendez, il est peu probable que deux échantillons qui viennent de la même population diffèrent autant ; ils ne viennent probablement pas de la même population : remettons en question cette hypothèse qui est tout à fait nulle !

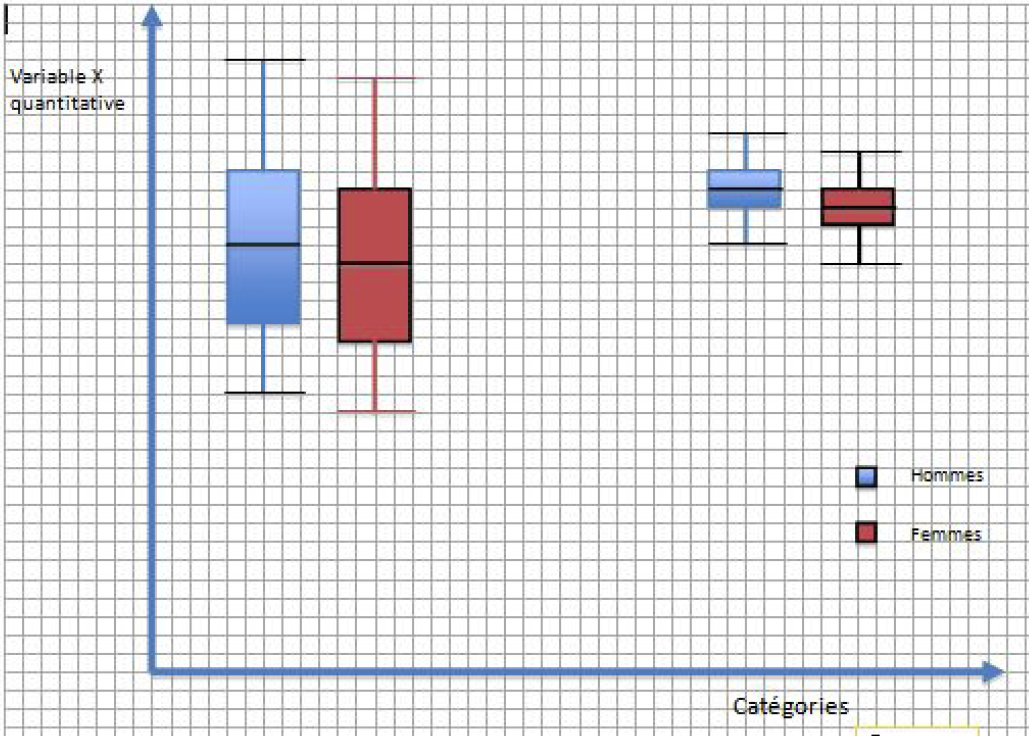
Mais c’est combien, un peu ? C’est combien, beaucoup ? Pour comprendre la différence entre un peu et beaucoup, nous allons dessiner les boîtes à moustache (box plots en anglais) qui représentent les deux échantillons, l’une en bleu et l’autre en rouge, comme dans le diagramme ci bas. Nous dessinerons la moyenne de l’échantillon dans la boîte à moustache (en général, c’est la médiane qui est indiquée dans une boîte à moustache mais nous voulons ici indiquer la moyenne).

Avec un logiciel comme OpenOffice (open source, gratuit), ou à la rigueur Word, on peut faire en sorte que ces boîtes à moustache soient facilement déplaçables dans le diagramme, une à une. Et on peut déplacer la boîte rouge, vers le haut ou vers le bas, pour que les moyennes des deux échantillons s’éloignent ou se rapprochent. Et là on peut observer deux choses, qui vont aider à raffiner l’intuition.

D’abord, on peut déplacer l’échantillon rouge vers le haut ou vers le bas, en demandant chaque fois aux étudiants si une différence entre les moyennes telle que celles qu’ils observent leur semble être petite (donc due au hasard du choix de l’échantillon), ou grande (donc indiquant que les populations d’où sont tirés les échantillons diffèrent). Ensuite on pourra contraster les échantillons de droite avec ceux de gauche. Une même différence qui semble petite à gauche semblera plus importante à droite : c’est parce que plus la dispersion est grande, plus des écarts importants, dûs au hasard, sont probables. En jouant avec ces diagrammes, on développe l’intuition des étudiants, et on les amène à formuler leurs conclusions en phrases complètes, ce qui renforce leur compréhension. Dans les deux cas, on fait le lien entre la différence observée et la position de cette différence dans la distribution d’échantillonnage. Et à chaque manipulation des boîtes sur le diagramme on demande aux étudiants : d’après vous, cette différence est-elle suffisamment exceptionnelle pour qu’elle tombe dans les 5 % les plus extrêmes ? Des fois ce sera Oui avec certitude, des fois Non avec certitude, et pour tous les cas incertains, on ne pourra pas décider.

Dans ces cas intermédiaires, la réponse ne sera pas claire. L’intuition a ses limites. Pour pallier les limites de l’intuition, il faudra recourir aux calculs statistiques précis fait par SPSS. Il ne sera pas nécessaire de faire des preuves mathématiques. Si l’intuition a bien été développée grâce aux exercices, on pourra comprendre le sens des tableaux de SPSS, en particulier celui de la colonne Sig. qui donne les probabilités de se tromper si on rejette l’hypothèse nulle. On montrera la signification des tableaux (et de la colonne Sig. en particulier) en lien avec le diagramme des boîtes à moustache.

L’INTERPRÉTATION DES RÉSULTAT
D’UNE ANOVA À DEUX FACTEURS

On peut montrer la signification de la notion d’effet principal et d’interaction entre facteurs dans une ANOVA à l’aide des diagrammes suivants. Ces illustrations doivent être faites avant de montrer le moindre calcul de la procédure ANOVA. Il faut d’abord comprendre le sens des relations qualitatives que l’on constate dans les diagrammes suivants. Après, on va regarder les tableaux des résultats de la procédure ANOVA pour savoir si les différences constatées intuitivement sont effectivement significatives, statistiquement, ou pas.

Donc, on mesure une variable X (disons la réduction du nombre de jours de grippe en hiver quand on prend de la vitamine C régulièrement), et on voit dans quelle mesure elle donne des résultats pour les hommes et pour les femmes, en contrastant le cas où on administre une forte dose de vitamine C, une faible dose, ou un placebo.

Les diagrammes A, B, C et D qui suivent illustrent les résultats possibles. Les trois modalités du premier facteur sont indiquées par la position sur le diagramme : à gauche, faible dose ; au centre, placebo ; à droite, forte dose. Les deux modalités du 2e facteur sont indiquées par la couleur : Hommes, bleu ; Femmes, rouge.

Dans le diagramme A, le facteur Traitement semble faire une différence, mais le facteur Genre ne semble pas faire de différence. En d'autres termes, selon le diagramme A), pour cet échantillon, une faible dose de Vitamine C a pour effet de diminuer le nombre de jours de grippe plus que le placebo, et une forte dose a un effet plus marqué qu'une faible dose. On dirait aussi que cet effet est pareil pour les hommes et pour les femmes. Mais comment savoir si cet effet est dû au choix de l'échantillon ou qu'il reflète quelque chose au niveau de toute la population ? C’est la statistique F qui nous le dit : pour chaque valeur de F, SPSS va nous donner la probabilité de l’obtenir si l’échantillon est aléatoire, sur la base d’une hypothèse nulle qui dit que tous les traitements produisent le même effet. Mais ici, on va fonctionner de façon intuitive : si les distributions ne s’écartent que de peu, on va considérer que les différences entre les groupes ne sont pas significatives. Une fois que l'idée sera claire, on ira voir ce que disent les tableaux de de l'ANOVA dans SPSS.

Ainsi, donc, le diagramme A nous dit que les méthodes de traitement produisent des différences significatives, mais qu’il n’y a pas de différence dans la variable dépendante entre les hommes et les femmes. Ont formulera la conclusion comme suit :

Effets principaux : Le traitement a un effet significatif sur la réduction du nombre de jours de grippe : une petite dose ainsi qu’une forte dose du traitement entraînent une plus forte réduction du nombre de jours de grippe que le placebo. La dose elle-même (faible ou forte) ne semble pas faire de différence significative. De plus, les hommes et les femmes semblent réagir de la même façon au traitement. Donc, il n’y a pas d’effet principal du sexe.

(Note : je dis « semble » car je ne me fie pas aux niveaux de signification donnés dans le tableau SPSS. La formulation de la conclusion sera plus précise lorsqu’on aura des données chiffrées)

Pour le diagramme B), on constate que l’effet principal expliquant les variations est le sexe. Il n’existe aucune différence significative entre les groupes ayant consommé le placebo ou le médicament.

Le diagramme C), quant à lui, serait interprété comme suit :

Le traitement a un effet principal significatif sur la réduction du nombre de jours de grippe : une petite dose ainsi qu’une forte dose du traitement entraînent une plus forte réduction du nombre de jours de grippe que le placebo. La dose elle-même (faible ou forte) ne semble pas faire de différence significative. De plus, les hommes et les femmes ne réagissent pas de la même façon au traitement, qui semble avoir un effet plus élevé sur les hommes que sur les femmes, quel que soit le traitement. Il y a donc un effet principal du sexe. Mais il ne semble pas y avoir d’interaction entre les deux facteurs.

(Note : je suppose ici que la différence entre les deux boîtes à moustache de droite, dans le diagramme C, n’est pas significative)

Le diagramme D serait interprété comme suit :

Le traitement a un effet significatif sur la réduction du nombre de jours de grippe : une petite dose ainsi qu’une forte dose du traitement entraînent une plus forte réduction du nombre de jours de grippe que le placebo. De plus, les hommes et les femmes ne réagissent pas de la même façon au traitement, et cette réaction au traitement n’est pas la même pour une dose faible ou forte : la dose faible est plus efficace pour les hommes, alors que la dose forte est plus efficace pour les femmes. En plus des deux effets principaux, il y a donc une interaction entre les deux variables.

EFFET PRINCIPAL SIMPLE

L'effet principal simple peut être illustré par ce qu'on observe dans le diagramme C entre deux des trois groupes d'hommes, ou deux des trois groupes de femmes. Ainsi, les hommes qui prennent une dose faible de Vitamine C connaissent la même réduction de jours de gripe que ceux qui prennent une dose forte. Il n'y a donc pas d'effet principal simple de la variable Traitement qui distinguerait les hommes qui prennent une faible dose ou une forte dose. Mais il y a un effet principal simple de la variable Traitement pour les hommes qui prennent de la Vitamine C en dose faible par rapport à ceux qui prennent un placebo. Idem pour la dose forte. De façon plus abstraite, la définition générale est la suivante : L'effet principal simple est l'effet qui produit une différence entre deux catégories d'une variable qui en a plusieurs, à l'intérieur d'un groupe défini par une modalité de la deuxième variable.

On peut examiner les trois autres figures en contrastant n'importe quels deux groupes d'hommes, ou n'importe quels deux groupes de femmes. Pour qu'il y ait une possibilité d'effet principal simple, il faut d'abord qu'il y ait un effet principal (tout-court) et que la variable ait trois catégories ou plus, pour qu'on contraste n'importe quelles deux des catégories.

Rappelez-vous cependant que pour tous les cas illustrés ci-haut, il n’y a qu’une seule façon de déterminer si les différences observées sont statistiquement significatives : il faut faire les calculs de la procédure ANOVA, et examiner les niveaux de signification calculés : s’ils sont plus petits que 0,05, ont en conclut que les différences observées sont statistiquement significatives. Sinon, elles ne le sont pas. SPSS peut faire ces calculs pour nous et on trouve les résultats dans la colonne intitulée Sig. des tableaux de l’ANOVA.

Passons maintenant à un autre exemple de l’utilisation des représentations visuelles, celui de l’analyse factorielle.

ILLUSTRATION DE LA DIMENSION
D'UN ENSEMBLE DE DONNÉES DANS
UNE ANALYSE FACTORIELLE

L'analyse factorielle vise à réduire le nombre de variables qui décrivent en ensemble de données, et à déterminer la dimension sous-jacente à cet ensemble de données. Par exemple, si on a un nuage de points qui représente des notes en chimie et en physique d'un groupe d'étudiants au secondaire, on constate que ces données ont en réalité une seule dimension, elles se retrouvent toutes distribuées le long d'un seul axe, qui représente la facilité qu'ont les étudiants en chimie/physique, puisque ceux qui sont bons dans l'une de ces deux matières ont tendance à être bons dans l'autre aussi. Donc, les variables Note en chimie et Note en physique représentent en réalité une seule et même compétence : facilité avec les sciences naturelles, qui se manifeste dans le cours de chimie et dans le cours de physique. Visuellement, on voit qu'une seule ligne exprime la tendance du nuage de point. On peut déterminer si quelqu'un a de bonnes notes en chimie et en physique si on connaît sa position sur cette ligne unique (qui se trouve à être la droite de régression). En fait ceci signifie qu'un seul facteur est capable d'exprimer la presque totalité de la variance observée dans les données. Le diagramme suivant illustre cette situation.

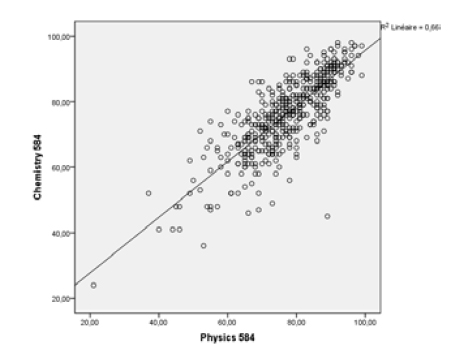
Les données illustrées par le nuage de point ont en réalité une seule dimension, puisqu’un seul axe permet de capter l’essentiel de la variation observée entre les données.

Ce qu’il faut voir ici, ce n’est pas la droite de régression. Il faut voir cette ligne autrement : comme un axe, le long duquel les données sont dispersées. Cet axe unique capte d’un seul coup la variation observée dans les notes en chimie et en physique. Si on pouvait calculer le score de chaque étudiant sur cet axe unique (on le peut), on remplacerait les deux variables (note en chimie et note en physique) par une seule nouvelle variable (considérée comme étant le premier facteur) qui permet d’exprimer la compétence des étudiants tant en chimie qu’en physique. Donc, l’ensemble de données que nous avons a en réalité une seule dimension et non pas deux, puisqu’un seul axe permet d’exprimer l’essentiel de la variation.

L’analyse factorielle vise à généraliser ce type de raisonnement à la situation où l’on a plusieurs variables. Mais comment visualiser la notion de 'réduction des variables' dans le cas de plusieurs variables ? Nous allons illustrer la méthode en prenant les données relatives à trois variables et en déterminant si elles ont une seule ou deux (ou trois?) dimensions sous-jacentes.

Nous allons travailler avec un fichier SPSS de données nommé : résultats scolaires ang réduit.sav.

Nous allons produire l’analyse factorielle pour plusieurs combinaisons de variables. Dans chaque cas, nous allons d’abord examiner le diagramme a trois dimensions que SPSS produit, et le manipuler pour faire le faire pivoter dans plusieurs directions. Si vous avez accès à SPSS, ouvrez le fichier mentionné, copiez les commandes suivantes dans la fenêtre de Syntaxe, et faites les rouler.

* Exemples de variables TRÈS fortement corrélées. L'intuition nous dit que c'est un seul facteur.

GRAPH

/SCATTERPLOT(XYZ)=vocss WITH tot_read WITH comprsx2

/MISSING=LISTWISE .

FACTOR

/VARIABLES vocss tot_read comprsx2

/MISSING LISTWISE /ANALYSIS vocss tot_read comprsx2

/PRINT INITIAL CORRELATION EXTRACTION

/PLOT EIGEN

/CRITERIA MINEIGEN(1) ITERATE(25)

/EXTRACTION PC

/ROTATION NOROTATE

/METHOD=CORRELATION.

* Exemples de variables fortement corrélées. Ce n'est pas clair si c'est un seul facteur ou deux.

GRAPH

/SCATTERPLOT(XYZ)=math536 WITH physsci WITH history

/MISSING=LISTWISE .

FACTOR

/VARIABLES math536 physsci history

/MISSING LISTWISE /ANALYSIS math536 physsci history

/PRINT INITIAL CORRELATION EXTRACTION

/PLOT EIGEN

/CRITERIA MINEIGEN(1) ITERATE(25)

/EXTRACTION PC

/ROTATION NOROTATE

/METHOD=CORRELATION .

* Exemples de variables fortement corrélées. On pourrait penser qu'il y a deux facteurs.

GRAPH

/SCATTERPLOT(XYZ)=math536 WITH vocrs WITH history

/MISSING=LISTWISE .

FACTOR

/VARIABLES math536 vocrs history

/MISSING LISTWISE /ANALYSIS math536 vocrs history

/PRINT INITIAL CORRELATION EXTRACTION

/PLOT EIGEN

/CRITERIA MINEIGEN(1) ITERATE(25)

/EXTRACTION PC

/ROTATION NOROTATE

/METHOD=CORRELATION .

GRAPH

/SCATTERPLOT(XYZ)=math536 WITH francmat WITH history

/MISSING=LISTWISE .

FACTOR

/VARIABLES math536 francmat history

/MISSING LISTWISE /ANALYSIS math536 francmat history

/PRINT INITIAL CORRELATION EXTRACTION

/PLOT EIGEN

/CRITERIA MINEIGEN(1) ITERATE(25)

/EXTRACTION PC

/ROTATION NOROTATE

/METHOD=CORRELATION .

Le diagramme obtenu pour la première commande GRAPH est le suivant :

On voit un nuage de points, mais on ne voit pas comment il est distribué dans l’espace. En cliquant deux fois sur le diagramme, on passe en mode Édition du graphique. Une icône dans le mode édition vous permet de faire pivoter le diagramme en cliquant et déplaçant la souris dessus. Le faire pivoter, c’est comme si on déplaçait l’angle à partir duquel on observe le nuage de points. Faites le pivoter dans diverses positions, pour obtenir, en bout de ligne, l’angle de vue que voici :

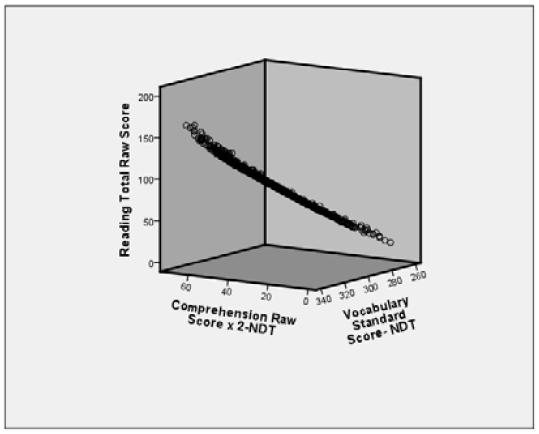
On peut constater, ici, que les points se trouvent tous dans un même plan ! Notre œil se trouve dans le même plan, donc, on ne voit qu’une mince ligne. Tous les points se trouvent à peu près dans ce plan. On constate que ces trois variables ont en réalité au plus deux dimensions, peut-être une seule. Pour le savoir, on va encore faire pivoter de façon à se mettre dans une position perpendiculaire au plan. On obtient ceci.

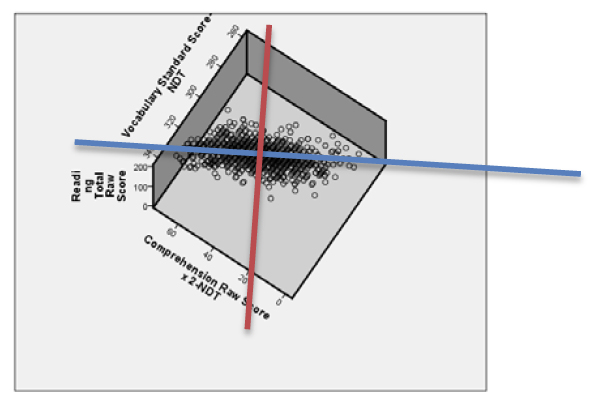
On voit que dans le plan où se trouvent les points, ils sont quand même regroupés autour d’une ligne (bleue), mais ils ne sont pas étroitement collés à cette ligne. Est-ce que la variation expliquée par la dimension perpendiculaire (ligne rouge) est assez importante, relativement ? En d’autres termes, ces points ont-ils une ou deux dimensions ? À l’œil nu, nous ne pouvons pas le dire. L’intuition a atteint sa limite. Il faut voir les tableaux produits par SPSS. Voici le tableau le plus important relatif à ce graphique.

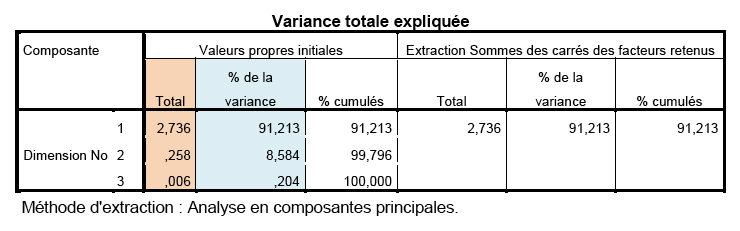
Dans la colonne intitulée % de la variance, SPSS donne le % de variance expliquée (ou captée) par chacun des facteurs. On voit que le premier facteur (axe bleu) représente 91 % de la variation des données ! Un deuxième facteur n’explique que près de 9 % de la variation, et le dernier, presque zéro. Dans la colonne de droite, SPSS ne liste que la variation expliquée par le premier facteur, et ignore les deux autres. Donc cet ensemble de données n’a qu’une seule dimension.

Si les variables originales sont standardisées, leur variance est égale à 1. La variance totale des variables standardisées est donc de 3 unités. La colonne intitulée Total, à gauche, représente la part de la variance totale des variables standardisées qui est expliquée par facteurs. Si la capacité explicative d’un facteur est moins de 1, cela signifie qu’il explique moins que sa part de variance… donc on ne le retient pas.

(Note : Cette quantité est appelée valeur propre à cause de la façon dont le calcul est fait : en effet, la démonstration de la procédure d’analyse factorielle est faite à l’aide du calcul matriciel, qui fait partie de l’algèbre linéaire. Ces valeurs se trouvent à être les valeurs propres de certaines matrices qui interviennent dans le calcul).

Dans les exemples suivants produits par la syntaxe, vous verrez que les 2^e et 3^e facteurs ont un rôle plus important, mais pas assez pour changer la conclusion de fond. Dans tous les cas, les données ont une seule dimension. Car il suffit qu’un seul facteur ait une bonne capacité explicative pour qu’il « déclasse » les deux autres dont la capacité explicative tombe au-dessous de la valeur 1. Quand il y a 4, 5 ou 6 variables, il est commun de déceler 2 ou 3 dimensions sous-jacentes.

CONCLUSION

Ce qu’il y a à retenir surtout des pages qui précèdent, c’est ceci :

On ne peut véritablement comprendre les statistiques en se fiant uniquement sur la lecture des tableaux, sur les preuves et procédures formelles, et sur les explications faites dans le langage courant. Il faut utiliser le langage visuel, qui permet de faire appel à l’intuition, de la développer, et de permettre de formuler des conclusions en termes qualitatifs. Ceci ne diminue en rien l’importance cruciale du formalisme et des preuves : les preuves, et les calculs précis qui en découlent, permettent de vérifier si l’intuition était bonne, et de corriger le tir au besoin. L’intuition peut nous induire en erreur et elle n’est certainement pas un critère de validation : seuls les calculs précis peuvent valider une hypothèse. Mais l’intuition, bien développée, permet d’anticiper les résultats, de mieux les comprendre, et en bout de ligne de mieux interpréter les résultats de calculs précis, appuyés par des preuves (faites ailleurs, par des spécialistes, sans doute) et de traduire en termes qualitatifs et conceptuels des résultats de calculs statistiques. L’intuition est donc absolument fondamentale dans la compréhension des résultats, dans leur reformulation par rapport aux problématiques de départ, et dans leur communication. Mais seuls les calculs précis, et justifiés théoriquement, fournissent les critères de validation des hypothèses statistiques.